Aufgabe 1 (5 P) Es sei f R2!R (Frechet) di erenzierbar in x, und xsei ein lokaler Minimalpunkt von f Warum ist dann Df( xE1=100(3 10 2)3 9 2 e1= 6For positive values of a and b, the binomial theorem with n = 2 is the geometrically evident fact that a square of side a b can be cut into a square of side a, a square of side b, and two rectangles with sides a and bWith n = 3, the theorem states that a cube of side a b can be cut into a cube of side a, a cube of side b, three a × a × b rectangular boxes, and three a × b × b

Complete Solutions Mathematical Methods In The Physical Sciences 3rd
X^2+(y-x^(2/3))^2=1
X^2+(y-x^(2/3))^2=1-X^2(y(x^2)^(1/3))^2 = 1 Natural Language;Jx y zj3e z 1 3!
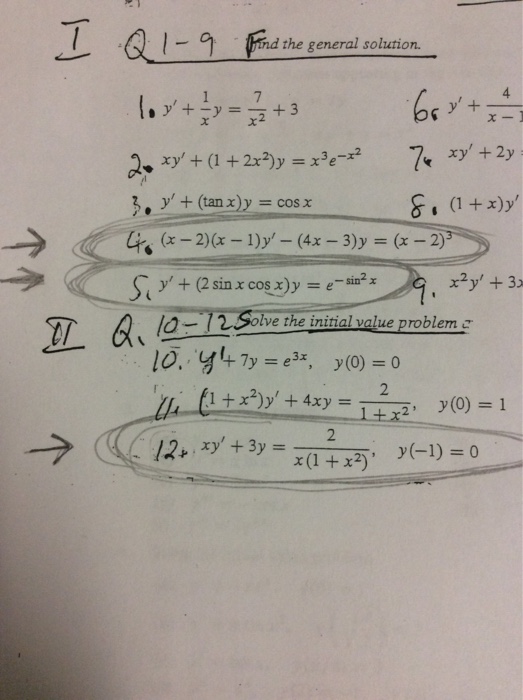



Find The General Solution Y 1 Xy 7 X 2 3 Chegg Com
Faktor x in den Ausdruck auf der linken Seite x (x 3) = 0 Für das Produkt x (x 3) werden gleich Null wir nedd zu haben x = 0 oder x 3 = 0 ;Beispiel 1 Lösen Sie die folgenden quadratischen Gleichung x 2 3x = 0 Lösung Beispiel 1 Angesichts x 2 3x = 0 ;Unlock StepbyStep (x^2y^21)^3=x^2y^3 Extended Keyboard Examples
1 cosg(x;y) 3x3 2cosy; Misc 15 If (𝑥 – 𝑎)^2 (𝑦 – 𝑏)^2= 𝑐2, for some 𝑐 > 0, prove that 〖1 (𝑑𝑦/𝑑𝑥)^2 /((𝑑^2 𝑦)/〖𝑑𝑥〗^2 )〗^(3/2)is a constant independent of a and bFirst we will calculate 𝑑𝑦/𝑑𝑥 (𝑥 – 𝑎)^2 (𝑦 – 𝑏)^2Betrachte die Gleichung (x 3)·(x 2)·(x 5) = 0 Es ist ein Produkt aus drei Faktoren (die Klammern), das 0 werden soll Ein Produkt ist genau dann 0, wenn mindestens ein Faktor 0 ist Man kann daraus schließen, daß mindestens eine Klammer 0 sein muß Es gibt drei Möglichkeiten 1 Klammer ist 0 x – 3 = 0 ⇐⇒ x = 3 2 Klammer ist 0 x 2 = 0 ⇐⇒ x = 2 3 Klammer ist 0 x
K = R2 = R×R (Ebene) K 3(x, y) Definiere ≺durch (x 1,y 1) ≺(x 2,y 2) ⇐⇒x 1 ≤x 2 Eigenschaften geordneter K¨orper (Folgerungen aus Axiomen) K geordneter K¨orper Proposition Fu¨r x,y ∈K sind aquivalent (i) x ≤y (ii) 0 ≤x−y (iii) x−y ≤0 (iv) −y ≤−x Proof (Ringschluss) KAPITEL 1 FOLGEN, KONVERGENZ, STETIGKEIT 3 (i) →(ii) Sei x ≤y Setze z = −x =⇒ (A) 0Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeDamit folgt ZZ Q y (1 x2y2)3=2 dxdy= Z 1 0 1 p 1x2 dx Z 1 0 1 p 2 dx = ln 1 p 2 ln 1 p 3 p 2 = ln 2 p 2 1 p 3 4a) Es gilt (vgl Figur) ZZ A x3y2 dxdy = Z R R Zp R2




Graph Graph Equations With Step By Step Math Problem Solver
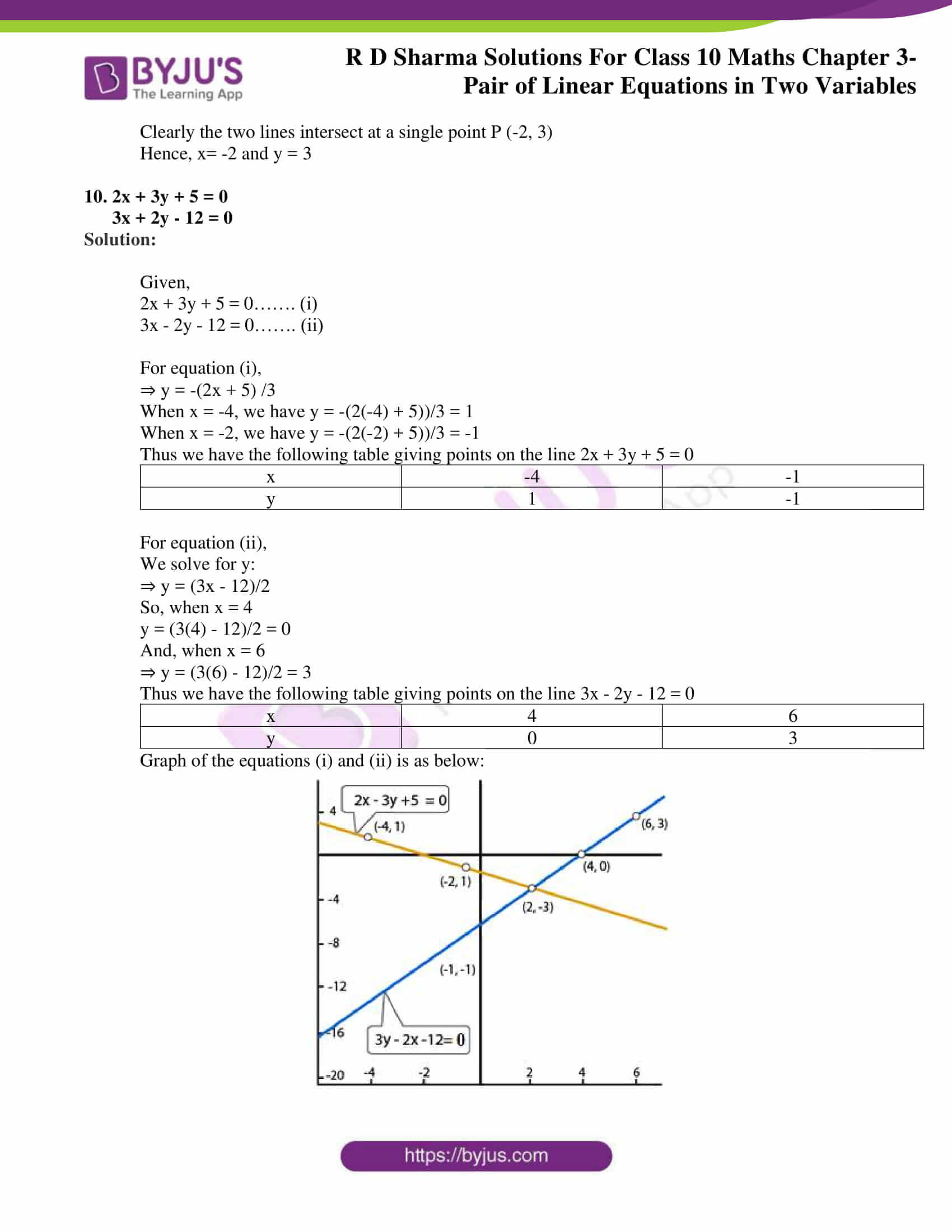



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2
Lösen Sie die obige einfache Gleichungen zu erhalten, die Lösungen x = 0 oder x = 3 Als Übung, überprüfen Sie, ob x = 02 Ubung zur Vorlesung¨ Lineare Algebra 2 I Hausaufgaben Abgabe Do, Aufgabe 1 Die symmetrische, nichtausgeartete Bilinearform β auf R3 sei gegeben durch β(x,y) = x1y1 x3y3 x1y2 x2y1 x2y3 x3y2 Bestimmen Sie eine Sylvesterbasis von R3 f¨ur β Aufgabe 2 Sei K ein K¨orper mit char(K) 6= 2 Sei V ein 2dimensionalerThe points (x,y,z) of the sphere x 2 y 2 z 2 = 1, satisfying the condition x = 05, are a circle y 2 z 2 = 075 of radius on the plane x = 05 The inequality y ≤ 075 holds on an arc The length of the arc is 5/6 of the length of the circle, which is why the conditional probability is equal to 5/6
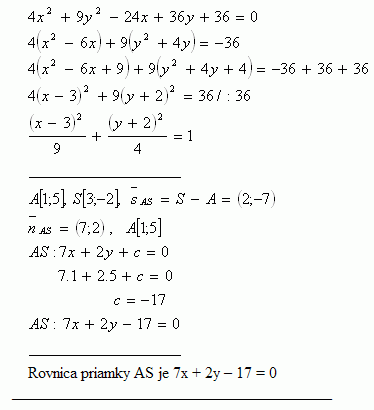



Kuzelosecky Vyresene Priklady




Is There A Solution For X For X 2 Y Sqrt 3 X 2 2 1 Mathematics Stack Exchange
X^2 2 y^2 = 1 Natural Language;Y=x3x212x No solutions found Rearrange Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation y(x^3x^212*x)=0 y'=(xy)^2 mit y(0)=0 ich hab schon versucht die homogene Dgl y'2xyy^2=0 durch substituion ( z=y^1) (Bernoullische Differentialgleichung) zu lösen, hat aber nicht funktioniert da ich später e^X^2 integrieren musste Das ist glaub ich auch nicht der richtige ansatz Ich hoffe mal das mir jemand helfen kann




The Solution Of 3x 1 X 2 Y 2dy Dx 2x 2 1 Y 3 A X 3is




Example 1 If X 1 Y 2 3 1 Find X And Y Class 11
Das Ausmultiplizieren dieses algebraischen Ausdrucks `(x2)^3` gibt `2^33*x*2^23*2*x^2x^3` zurück; 3 0 Answers #1 0 Oder ist x²y²=1 richtig ?Aufgabe 4 KürzenSiesoweitwiemöglich a) 144 168 b) 42ab2c 22a2bc füra,b,c6= 0 c) −x2y −2yx fürx6= 2 y d) 3xu−4xv6yu−8yv xv−3xu2yv−6yu fürx6=−2y,v6= 3 u Lösung a) 144 168 = 36 42 = 6 7 b) 42ab2c 22a2bc 21b 11a c) −x2y −2yx −x2y −(−x2y) = −1 d) 3xu−4xv6yu−8yv xv−3xu2yv−6yu x(3u−4v)2y(3u−4v) x(v−3u)2y(v−3u) (x2y)(3u−4v)(x2y)(v−3u)




Y 1 2 Y 1 2 Y 1 Y X 2 X Y Y 1 2 Y 3 1 3 Ppt Download
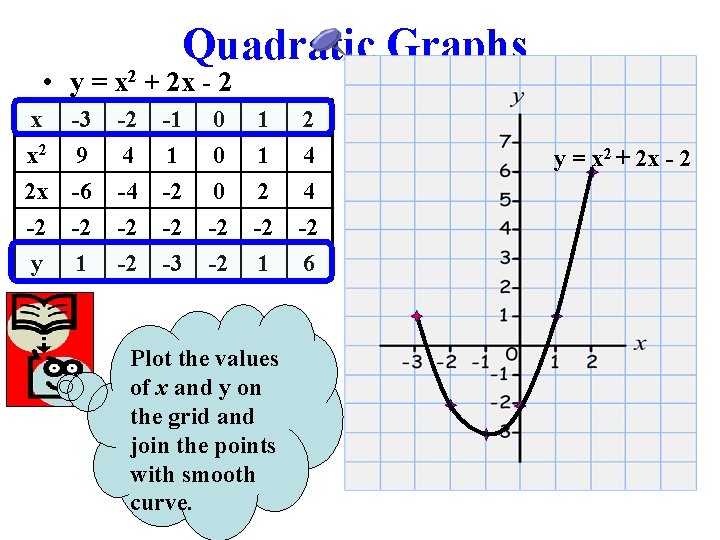



Quadratic Graphs Parabolas 1 To Draw A Quadratic
2 3 X Y x=y2 y=x2 (1,1) (4,2) Figure 2 The area between x = y2 and y = x − 2 split into two subregions If we slice the region between the two curves this way, we need to consider two different regions Where x > 1, the region's lower bound is the straight line For x < 1, however, the region's lower bound is the lower half of the sideways parabola The left end of the region is at x1 Grenzwerte und part Ableitungen Man untersuche die Funktion f(x;y) = x2eyy2 cosx x2y2 fur¨ (x;y) 6= (0 ;0) 1 fur¨ (x;y) = (0;0)auf Stetigkeit und ermittle die partiellen Ableitungen im Ursprung Außer in (0;0) ist f mit Sicherheit stetig Nun f¨uhren wir Polarkoordinaten ein und erhalten2 Aufgabe (a) DefiniereA n= f(x;y) 2R2 jx2y2




What Is The Axis Of Symmetry For The Parabola Y Chegg Com



Http Home Pf Jcu Cz Lsamkova Ma5sedme Pdf
Suppose k \neq 1, Then the expression is \frac{1k^2}{1k^3} \lim_{x \to 0} \frac1x However, we know that \lim_{x \to 0^} \frac1x = \infty and \lim_{x \to 0^} \frac1x = \infty Suppose ∣ k ∣ = 1, Then the expression is 1 − k 3 1 − k 2 lim x → 0 x 1 However, we know that lim x → 0 x 1 = ∞ and lim x → 0 − x 1 = − ∞ 8x^2y^2/4x^3y^3 8 x 2 y 2 / 4 x 3 y 3 https//wwEinsetzverfahren (2) 1 Einsetzverfahren (2) I a1·xb1·y = c1 II a2·xb2·y = c2 • Gleichung I oder II nach x oder y auflösen • Term in die andere Gleichung einsetzen • Gleichung nach der Unbekannten auflösen • zweite Unbekannte berechnen I 3x 5y = 19 II 7x 5y = 31 I nach x auflösen 3x 5y = 19 3x 5y = 19 / − 5y 3x = 19 − 5y / 3 x = 61 3 − 12 3 y I in II 7(61 3 − 12 3Y (1x 2y)3=2 dxdy= Z 1 0 Z 1 0 y (1x2 y2)3=2 dydx = Z 1 0 1 p 1x 2y 1 y=0 dx Für a>0 erhalten wir mit der Substitution u= x p ax2 Z 1 0 dx p ax2 = Z 1 p a1 p a du u = ln 1 p a1 p a Siehe nächstes Blatt!
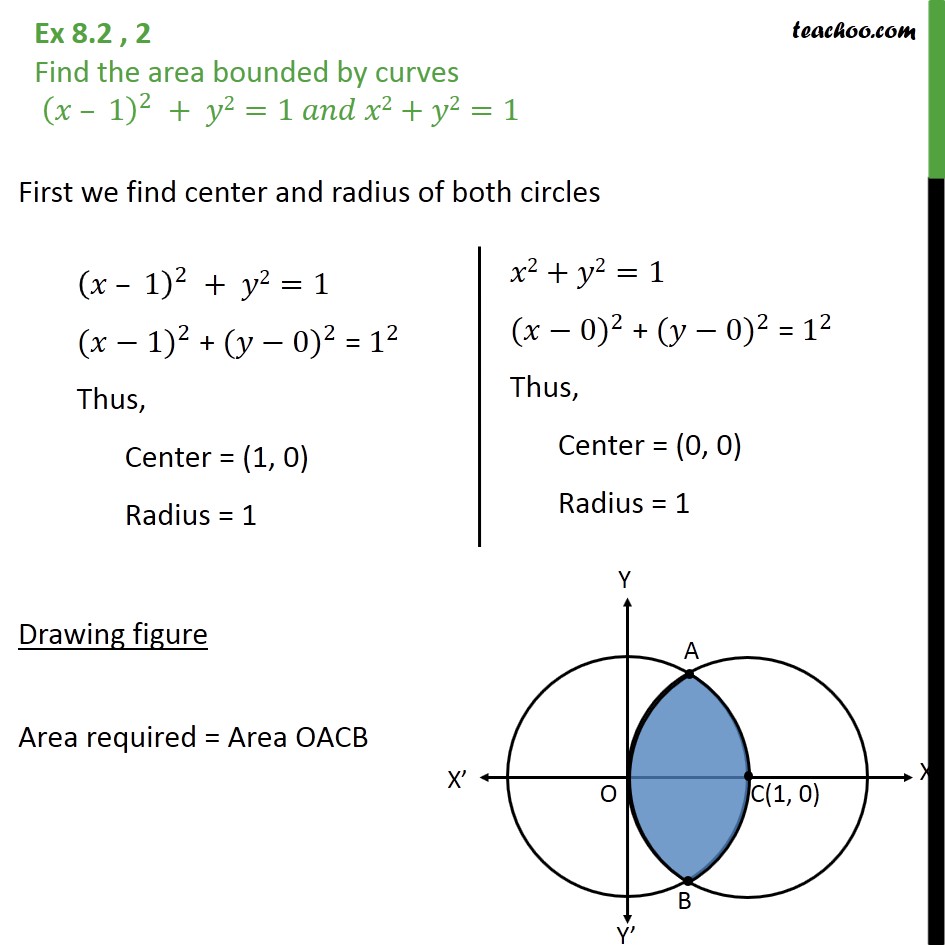



Ex 8 2 2 Find Area Bounded By X 1 2 Y2 1 And X2 Y2 1




If X 2 Y 2 1 And P 3x 4x 3 2 3y 4y 3 2 Then P Is Equal To
L osung De nition 53 auf S52 Die FourierTransformation einer Funktion f(x) ist de niert durch f^(y) = 1 (2ˇ)n=2 R Rn f(x)e ihx;yidnxwobei hx;yi= x 1y 1 x ny n Nach dem Satz 53, (Fou1), ist die FourierTransformierte f^(y) wohlde niert und stetig, vorausgestzt dass f(x) Lebesgueintegrierbar ist Aufgabe 4 (2 Punkte 2 Zusatzpunkte) 4a Formulieren Sie die H olderPlot x^2y^2x Natural Language; Probably you can recognize it as the equation of a circle with radius r = 1 and center at the origin, (0,0) The general equation of the circle of radius r and center at (h,k) is (x −h)2 (y −k)2 = r2 Answer link




Graphing X 3 2 Y 3 2 1 Mathematics Stack Exchange




X 3 2 Y 2 7 1 X 2 11 Y 3 11 1 Solve The Equation Brainly In
Die Gleichung sqrt(3)=3 y führt zu y=1/2 oder log 3 sqrt(3)=1/2 Die Gleichung 1/3=3 y führt zu y= 1 oder log 3 (1/3)= 1 Drei Logarithmen top Von Bedeutung ist die Logarithmusfunktion, wenn die Basis 2, e (eulersche Zahl) oder 10 ist Nach ISO 3111 gibt es für die zugehörigen Funktionsterme einfachere Schreibweisen, nämlich log 2 (x)=lb(x), log e (x)=ln(x) und log 10 (x)=lg(x) lb(x2x y = 9 2x x 2y = 10 x 2 Wird zu y = 9 2x y = 5 05x Gerne Fast aber 4x x = 7 2 Frage zu diesem Foto y= 2x 2,5 voi cool, goi? Ex 32, 11 If x 8(2@3) y 8(−1@1) = 8(10@5) , find values of x and y x 8(2@3) y 8(−1@1) = 8(10@5) 8(2𝑥@3𝑥) 8(−𝑦@𝑦




Ex 2 1 1 If X 3 1 Y 2 3 5 3 1 3 Find X And Y




Solve 1 X 2 D 2y Dx 2 X Dy Dx Y X 1 X 2 3 2 Mathematics 2 Question Answer Collection
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledgeGefragt von Derso 📘 Siehe "Differentialgleichungen" im Wiki 2 Antworten 1 Daumen Beste Antwort Differentialgleichung x 2 *y'=y 2Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel



Search Q Y 3d1 X Tbm Isch



Http Web Natur Cuni Cz Kunck6am 1819zs B1 09 Reseni Pdf
Versuche aber zB mal Nullfolgen x_n und y_n zu finden, sodass f(x_n,y_n) nicht gegen 0 geht mfg Gockel mfg Gockel Nachricht wurde editiert von fed am Der wissenschaftliche Taschenrechner im Internet Ideal zum Lösen von Hausaufgaben aus den Gebieten Mathematik, Physik und Technik Mit Vektor/Matrixrechner, Gleichungslöser, komplexen Zahlen und Einheitenumrechnung(jxj jyj jzj)3e 1 3!




Unit 2



Q Tbn And9gcsl0jyluxfxjjcizs7jyiyflsxbm6hpbpzdawckl4kjhmo0pmir Usqp Cau
(x 2y)3= @f @x (@f @y) = 1 2 @f @x (p1 x2y) = 1 2 0 p x2y px x2y x 2y = 2 x ( y)3= @2f @x 2 = 1 p x2y xpx x2y x y = (x 2y) x2 (x2y) p x2y = y (x y)3= @2f @y 2 = 1 2 @f @y (p x2y) = 2 0 p x2y p1 1 2 x2y (x y) = 1 4 x 2y)3= 3 Serie bis Mo, 2 5 11 ;Das Ausmultiplizieren des folgenden Produktes `(3x1)(2x4)` wird `3*x*2*x3*x*42*x4` zurückgesendet;3 Signals and Systems Part II Solutions to Recommended Problems S31 (a) xn= 8n 8 n 3 n 0 1 2 3 Figure S311 (b) xn = unun 5 0041T 0 1 2 3 4 5




If Y 2x 3 2 X 1 2 2 X 1 2 1 Then Dy Dx Is



How Do You Solve The System X 2y 1 And X 2 Y 2 25 By Graphing Socratic
= −2(1tan2(x))/y3 1 Somit gilt ∂ ∂y ∂ ∂x f(x,y) = ∂ ∂x ∂ ∂y f(x,y) und die Bedingung an die gemischten zweiten Ableitungen nach Schwarz ist erf¨ullt 2 Da gilt tan0(x) = 1 tan2(x) und ∂ ∂x f(x,y) = tan2x1 y2 y setzen wir an fˆ(x,y) = tan(x)/y2 xyg(x), es gilt ∂ ∂x fˆ(x,y) = ∂ ∂x f(x,y)g0(x) Somit folgt g0(x) = 0 und f(x,y) = tan(x)/y2 xy cGraph x^2y^2=1 x2 − y2 = −1 x 2 y 2 = 1 Find the standard form of the hyperbola Tap for more steps Flip the sign on each term of the equation so the term on the right side is positive − x 2 y 2 = 1 x 2 y 2 = 1 Simplify each term in the equation in order to set the right side equal to 1 1 The standard form of anEs ist zu beachten, dass das Ergebnis nicht in seinem einfachsten Ausdruck zurückgegeben wird, um den Schritten der Berechnung folgen zu können



Graph Equations System Of Equations With Step By Step Math Problem Solver




How Do You Solve X 1 2 Y 2 3 4 And X 2y 5 Socratic
Aufgabe 57 a) Für f(x,y) = 3 p x3y 6= 0 0 x= 0 giltimPunkt(0,0) •StetigkeitDadiedritteWurzelstetigist,gilt lim kxk→0 f(x,y) = 3 r lim kxk→0 (x3 y3)= 0 = f(0,0) Somitistfstetigin(0,0) •partielleDifferenzierbarkeit f x(0,0) = lim h→0 f(0h,0)−f(0,0) h = limSOLUTION 1 Begin with x 3 y 3 = 4 Differentiate both sides of the equation, getting D ( x 3 y 3) = D ( 4 ) , D ( x 3) D ( y 3) = D ( 4 ) , (Remember to use the chain rule on D ( y 3) ) 3x 2 3y 2 y' = 0 , so that (Now solve for y' ) 3y 2 y' = 3x 2, and Click HERE to return to the list of problems SOLUTION 2 Begin with (xy) 2 = x y 1 Differentiate both sidesA B(x 1) C(y 1) = (x 1 2 y 1 2) A B(x 2) C(y 2) = (x 2 2 y 2 2) A B(x 3) C(y 3) = (x 3 2 y 3 2) Wenn man soweit ist, erhält man x m = B/2, y m = C/2, und r 2 = x m 2 y m 2 A Beispiel Gesucht werden Mittelpunkt und Radius des Kreises, der durch die Punkte (24), (13) und (57) geht Wir stellen das Gleichungssystem auf A 2B 4C = A B 3C = 10 A
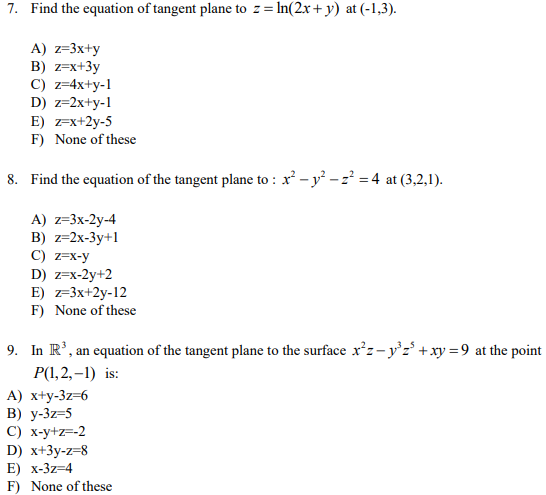



7 Find The Equation Of Tangent Plane To Z Ln 2x Chegg Com
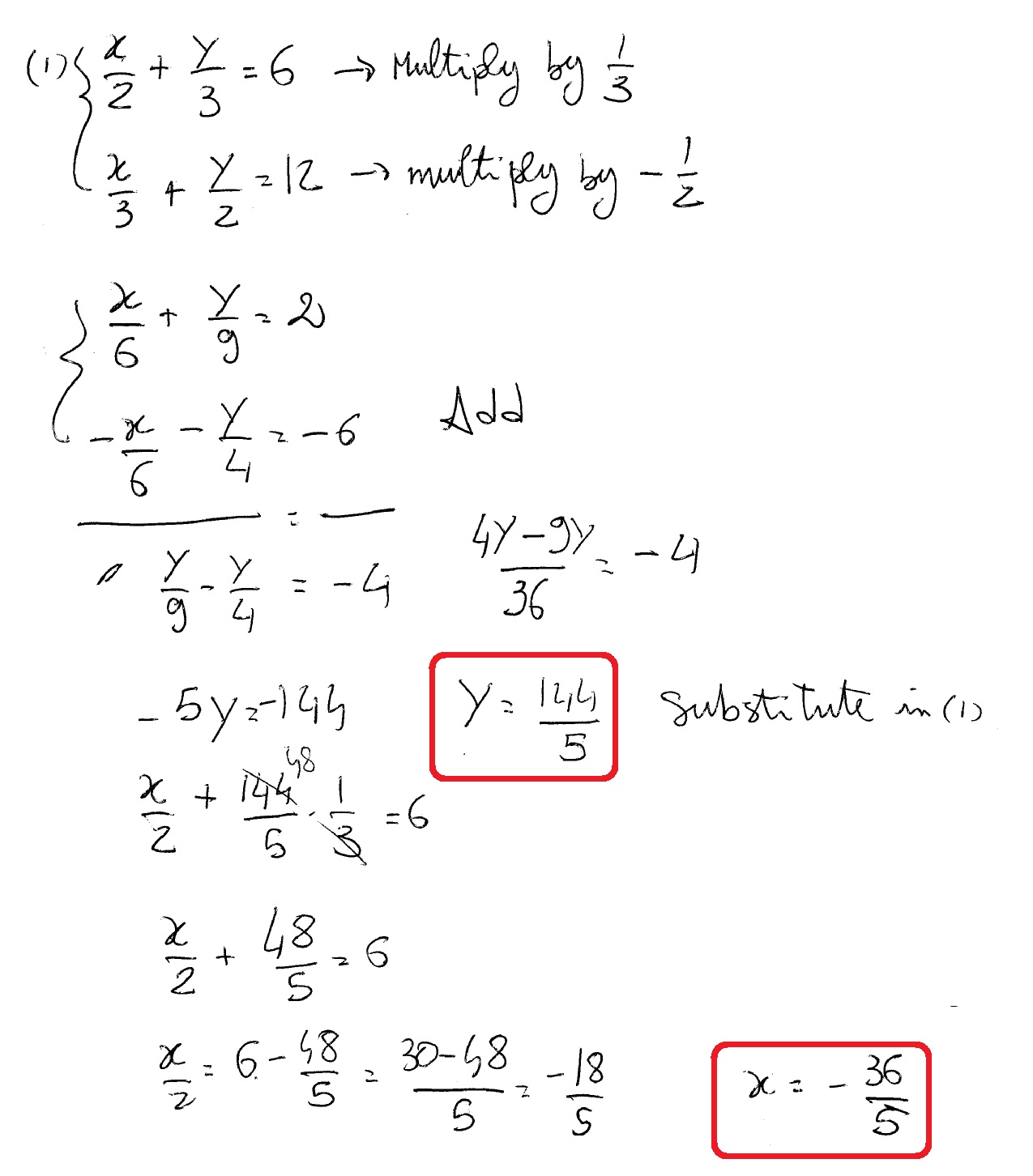



How Do You Solve X 2 Y 3 6 And X 3 Y 2 12 Socratic
f (x,y)=x^3/ (x^2y^2) Stetig differenzierbar Meine Frage Hallo, ich konnte leider an dem wo Differenzierbarkeit im R^n angefangen wurde nicht zur Uni und wollte mich deshalb zum einen vergewissern, ob ich die Herangehensweise richtig verstanden habe und zum anderen wollte ich wissen, wie man mit der Stetigkeit bei der Aufgabe weiter kommt2xsiny Aufgabe 2(4 Punkte) Bestimmen Sie Maximum und Minimum der Funktion f(x;y;z) = x2 y2 (z 1)2 auf dem Ellipsoid S= f(x;y;z) 2R3 x2 (y 2) 2 (z 3) 2 = 1g Hinweis Diese Aufgabe l asst sich wie in dem Beispiel der Vorlesung vom 181 diskutieren Dazu eliminiere man geeignet eine Variable in der Funktion und bestimme den De nitionsbereich(x2)(x3)(x3)(x2)=4(x1) Two solutions were found x = 4 x = 2 Rearrange Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation More Items Share Copy Copied to clipboard 2\left(32x2\right)=3x2\left(x\left(32x\right)\right) Use the distributive property to multiply 2 by x1 2\left(12x\right)=3x2\left(x\left(3




Keep Calm And X 2 Y 2 1 3 X 2y 3 0 You Poster Boronuraniumnitrogengallium Keep Calm O Matic



Http Web Natur Cuni Cz Kunck6am 1819zs B1 09 Reseni Pdf
Simplify (xy)(x^2xyy^2) Expand by multiplying each term in the first expression by each term in the second expression Simplify terms Tap for more steps Simplify each term Tap for more steps Multiply by by adding the exponents Tap for more steps Multiply by Tap for more steps Raise to the power of Use the power rule to combine exponents Add and Multiply by 3,7k Aufrufe Differentialgleichungen Man betimme eine Funktion \( y(x) \), die der folgenden Differentialleichung nbest Anfangsbedingung genügt \( x^{2}y' = y^2 \) und \( y(1)= \frac{1}{2} \) differentialgleichungen; Oder du lässt \(x^2(y\sqrt3{x^2})^2=1\) plotten Kommentiert von racine_carrée Bitte logge dich ein oder registriere dich , um zu kommentieren
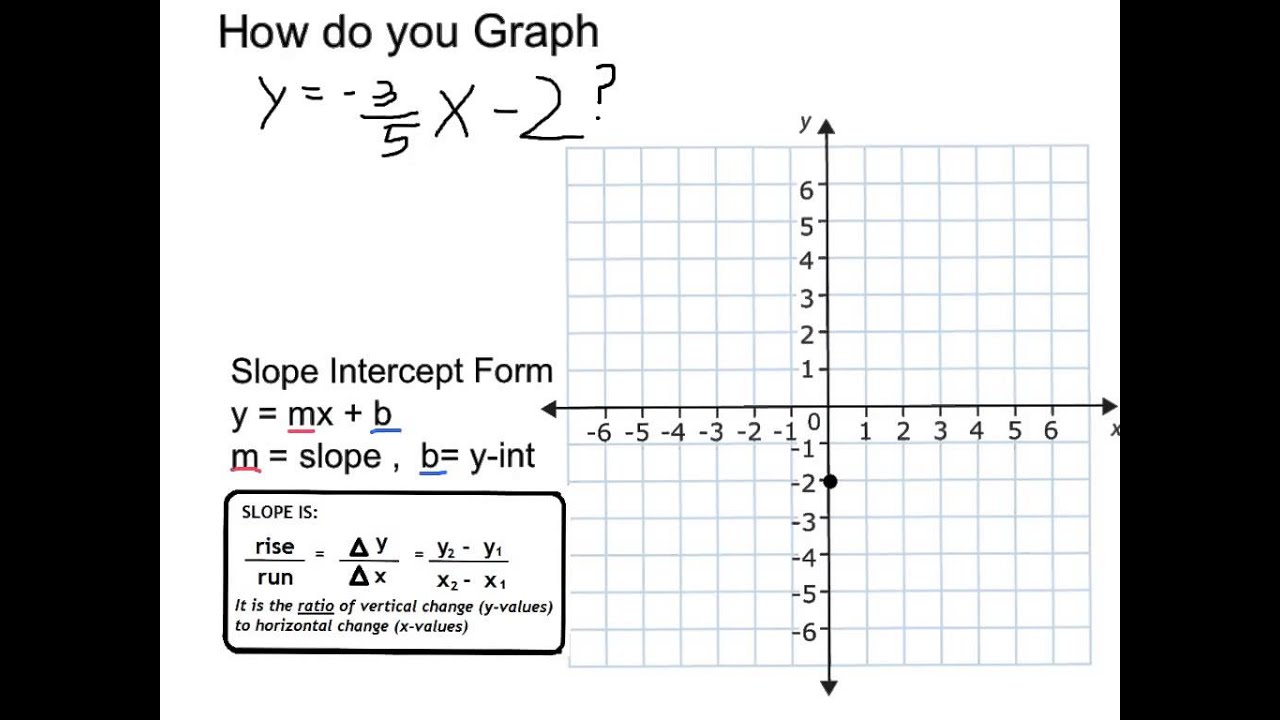



Graph Y 3 5 X 2 Youtube




Chapter 1 Practice Exercises
Bin extrem schnell wütend bzw auf 100 Heute zb war halt etwas nicht so wie geplant/e Ich würde dir raten zum Psychologen zu gehen vielleicht weiß er was er machen kann und kann mit 6 3 Markiere folgende Wörter undY=x2, y=x2, y=x2 und y=x2 Sie gelten jeweils nur für die oben bestimmten Bereiche Dieses Beispiel entspricht der teilweise hochgeklappten Parabel mit p(x) = x²1Radix #2 0 Ja ich meinte x^2y^2=1 aber wenn ich (1x^2)^1/2 eingebe kommt etwas ganz anderes raus Gast #3 0 Du hast recht, aber da kann ich dir leider auch nicht helfen Wenn du aber y^2 = 1 x^2 eingibst, kommst du natürlich wieder auf den Kreis Gruß radix !



1




If X Y Lies On Circle X 2 Y 2 1 Then Maximum Value Of X Y 2 Youtube
Use value of y in (1) x/2{2×(3)}/3=1 x/26/3=1 x/22=1 x/2=12 x/2=1 x=1×2 x=2 Hence, solution is x=2 and y=3 Hope it helps you, Please mark me as brainlist New questions in Math good morning aparuparava have a nice dayI am also fine how are you 1 Find k if the equation x 2y 22=0, x3y32= 0,2xy z = 0 have only trivial solution gm guys kise ho y = 4e^ (x^3/3) 1 dy/dx=x^2(1y) This is separable 1/(1y) dy/dx=x^2 int \ 1/(1y) dy/dx \ dx = int \ x^2 \ dx int \ 1/(1y) \ dy = int \ x^2 \ dx ln (1y) = x^3/3 C 1y = e^ (x^3/3 C) = e^ (x^3/3)e^C = Ce^ (x^3/3) y = Ce^ (x^3/3) 1 Applying the IV 3 = C e^0 1 = C 1 implies C = 4 y = 4e^ (x^3/3) 1 Calculus Science Anatomy & Physiology Astronomy Astrophysics BiologyExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel
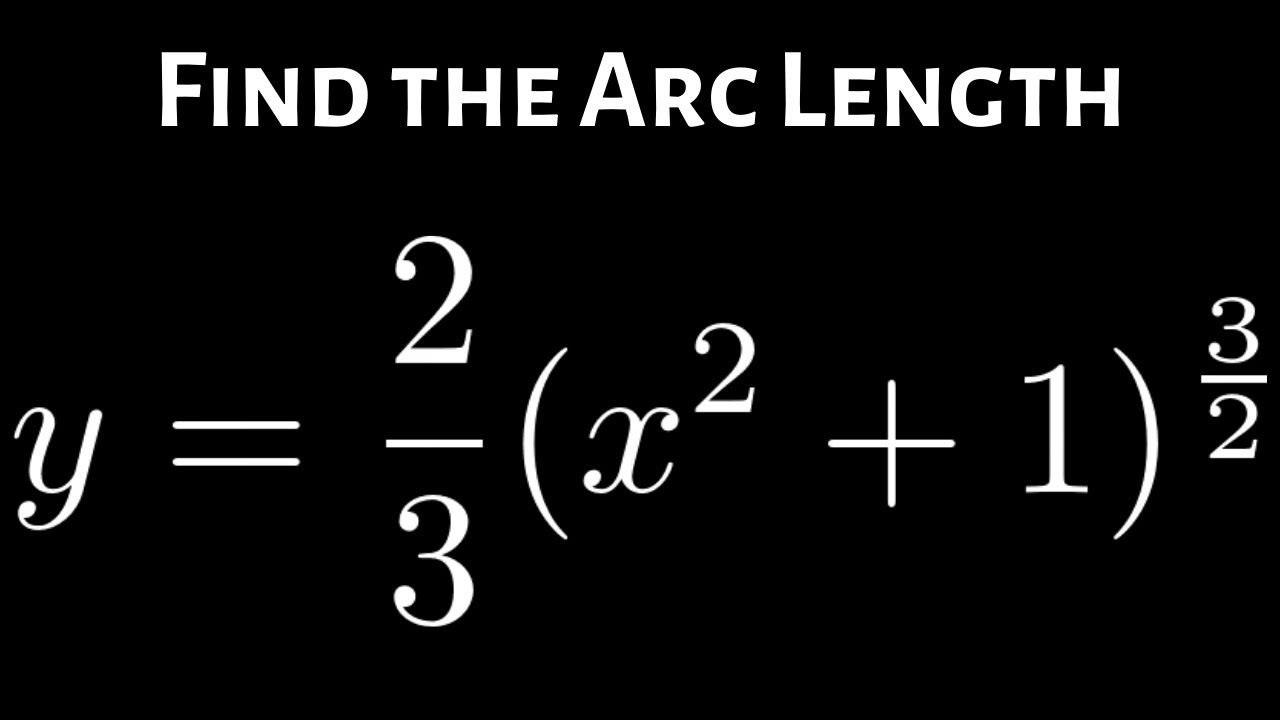



Find The Arc Length Y 2 3 X 2 1 3 2 Over 0 3 Youtube



What Is The Graph Of X 2 Y 3 X 2 2 1 Quora



What Is The Graph Of X 2 Y 3 X 2 2 1 Quora



Implicit Differentiation




Factorizing If 2x 1 Is A Factor Of The Expression 6 X2 5x




Ex 3 2 9 Find X And Y If 2 1 3 0 X Y 0 1 2 Ex 3 2




Ex 4 6 11 Solve Using Matrix Method 2x Y Z 1 X 2y Z 3 2 3y 5z 9



At What Points On The Curves X2 Y2 2x 4y 1 0 The Tangents Are Parallel To The Y Axis Studyrankersonline




If The Lines X 1 Y 2 Z 3 X 1 3 Y 2 1 Z 3 4 And X K 3 Y 1 2 Z 2 H Are Concur Youtube




File Heart Plot Svg Wikimedia Commons



Math Spoken Here Classes Quadratic Equations 3




If Y 1 X 1 X 2 2 X 3 3 Then Dy Dx A Y 1 B Y 1 C Y D Y 2
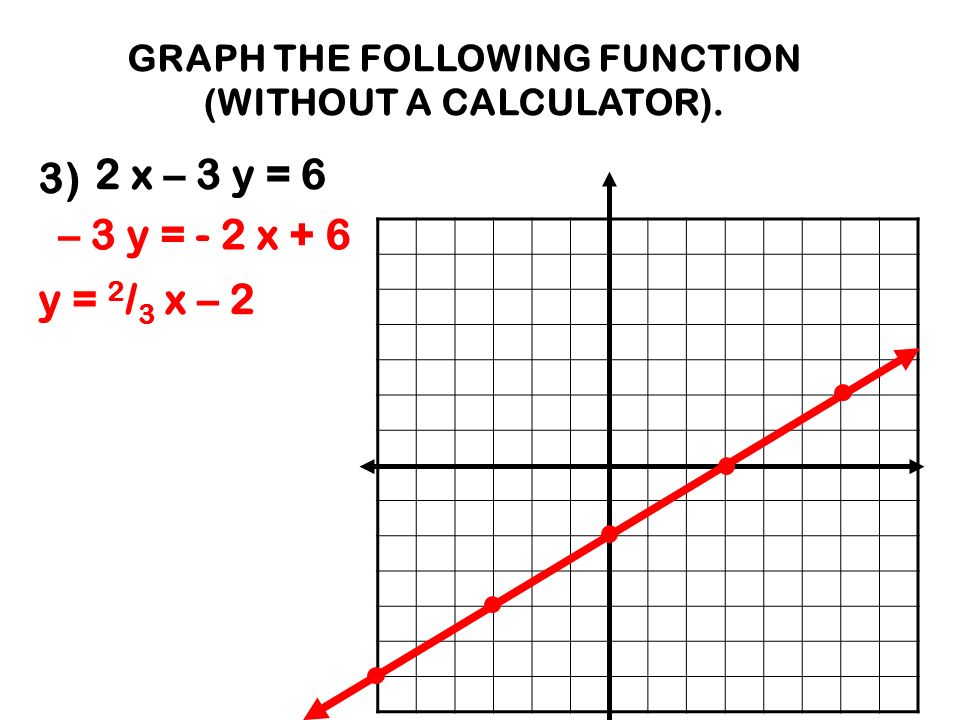



Graph The Following Function Without A Calculator 1 Y 3 X 2 2 X 1 1 Find The Vertex Y 3 1 3 2 2 1 3 1 Y 4 3 V Ppt Download




Find The Equations Of All Lines Having Slope 0 Which Are Tangent To The Curve Y 1 X 2 2x 3 Mathematics Shaalaa Com



Find The General Solution Y 1 Xy 7 X 2 3 Chegg Com
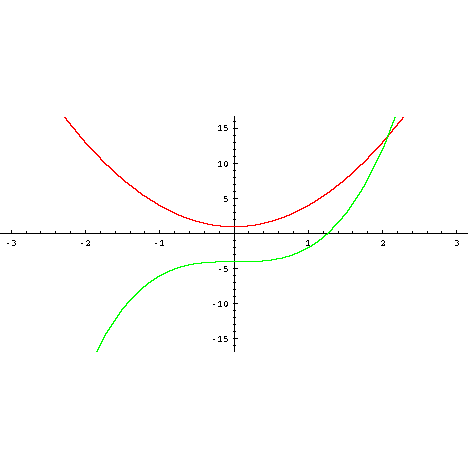



Graph Equations System Of Equations With Step By Step Math Problem Solver




Mrs Rivas Ppt Download




Solving Quadratics By Substitution Y 2 X 6 0 X Y 0 Solve For X Or Y Plug In The Expression For Y Simplify And Combine Like Terms Solve The Quadratic Ppt Download



How To Solve The System X 2 Y 2 25 And Y 3 4x Quora




Find X And Y If 2x 3y 2 3 4 0 And 3x 2y 2 1 1 5 Mathematics Shaalaa Com




Sketch The Circles Y 2 X 2 1 And Y 2 X 3 2 4 There Is A Line With A Positive Slope That Is Tangent To Both Circles Determine The




Graphing X 3 2 Y 3 2 1 Mathematics Stack Exchange




7 The Unit Hyperbola X 2 Y 2 1 Parameterized By The Functions X Download Scientific Diagram




Complete Solutions Mathematical Methods In The Physical Sciences 3rd



What Is The Vertex Of Y 2 X 3 2 1 Example




Algebra Calculator Tutorial Mathpapa
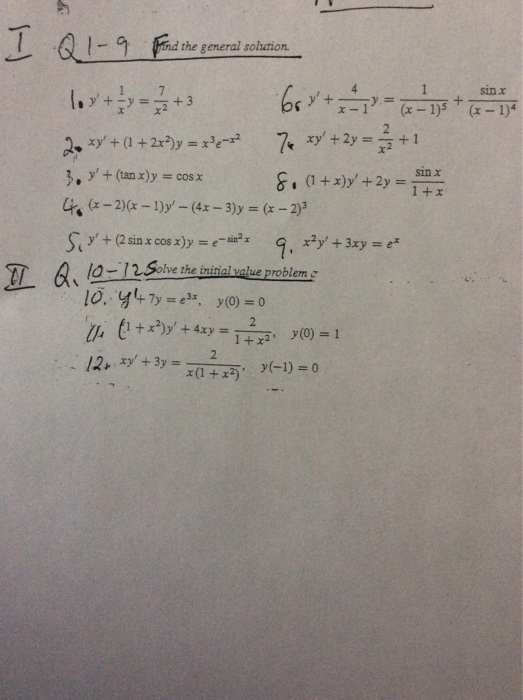



Find The General Solution Y 1 X Y 7 X 2 3 Chegg Com



Find The Shortest Distance Between The Following Pair Of Lines X 1 2 Y 2 3 Z 3 4 X 2 3 Y 3 4 Z 5 5 Sarthaks Econnect Largest Online Education Community



Sites Levittownschools Com Cbergersen Documents Unit 2 hw answers Pdf




If 1 X 2 Y 4 And 3 Y 1 X 11 Then
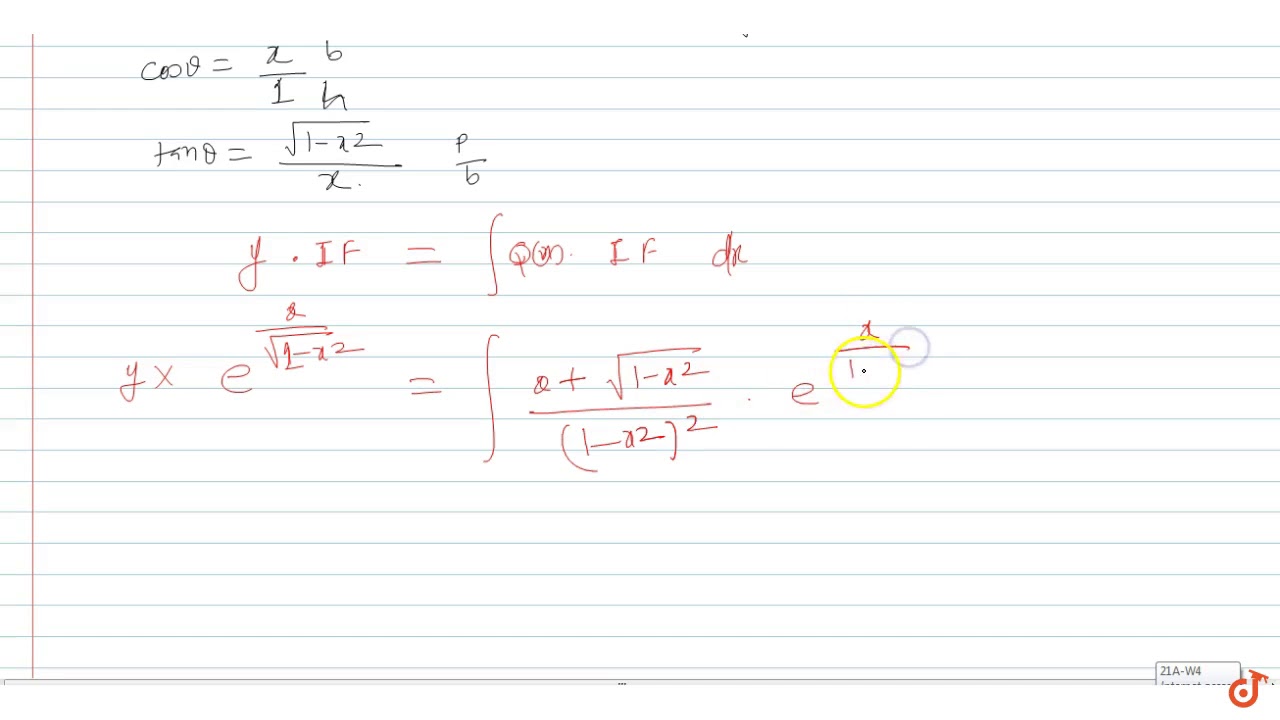



Solve Dy Dx Y 1 X 2 3 2 X 1 X 2 1 2 1 X 2 2 Youtube



1
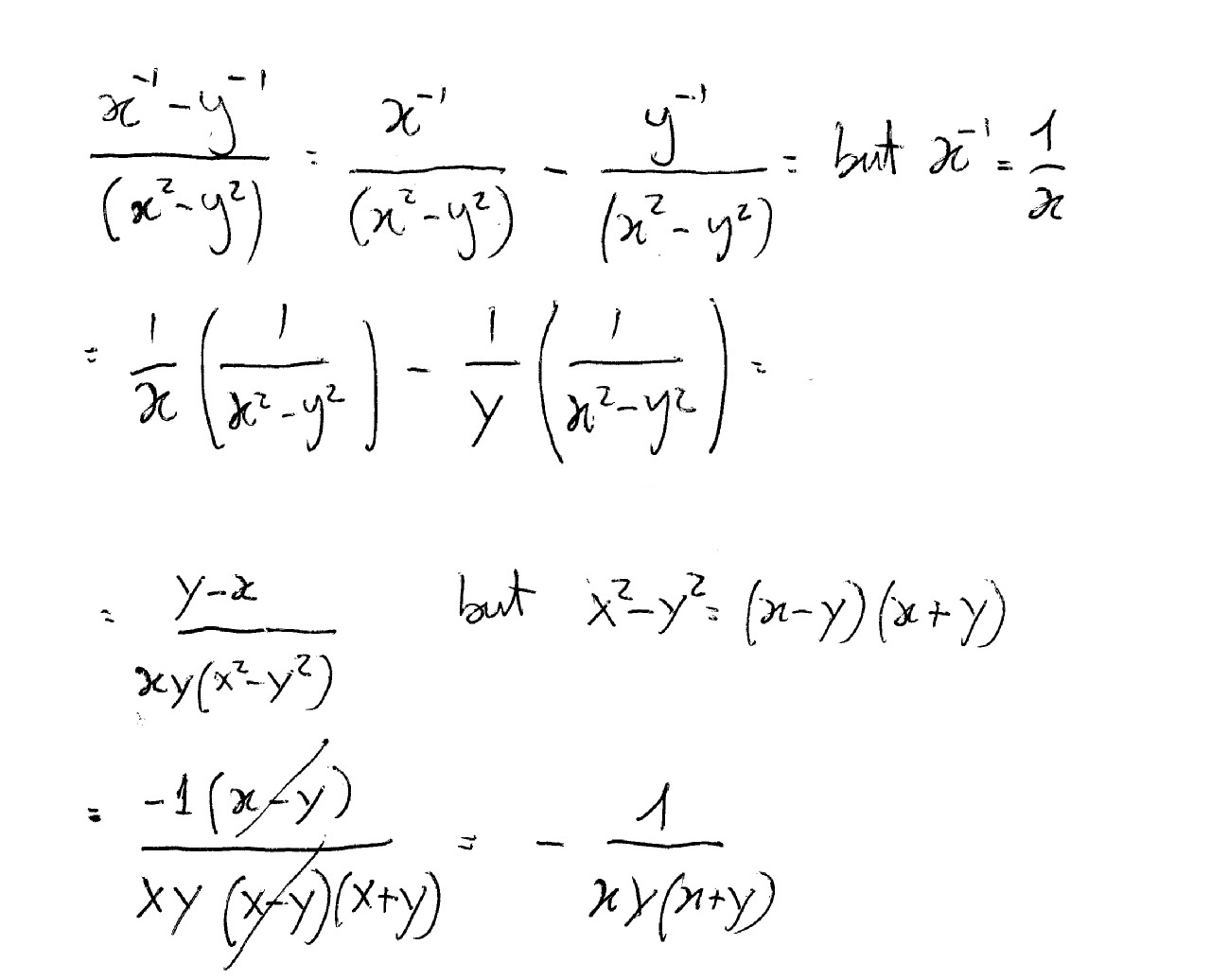



How Do You Simplify X 1 Y 1 X 2 Y 2 Socratic




2 X 2 3y 1 6 And 3 X 2 Y 0 Problem Set 1 Q6 1 Of Linear Equation In Two Variables Youtube
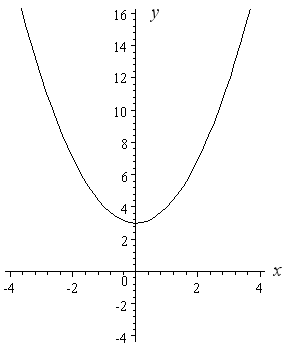



How To Draw Y 2 X 2 Interactive Mathematics
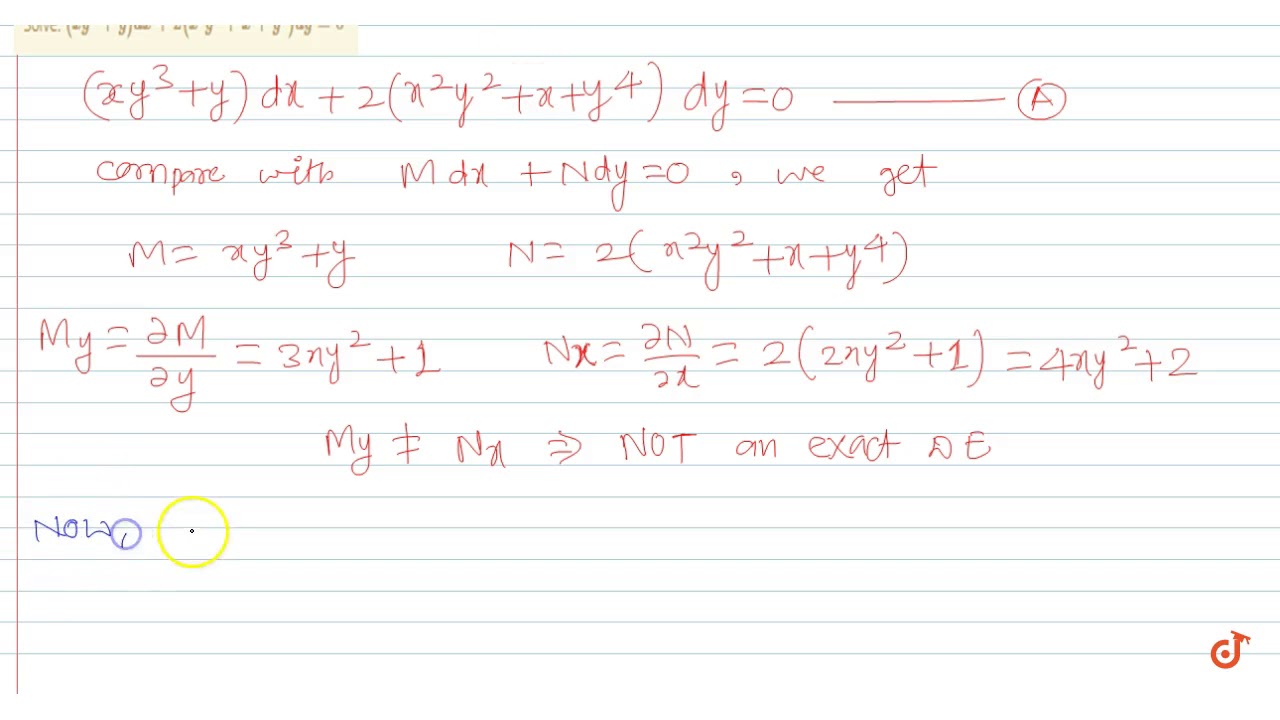



Solve Xy 3 Y Dx 2 X 2y 2 X Y 4 Dy 0 Youtube
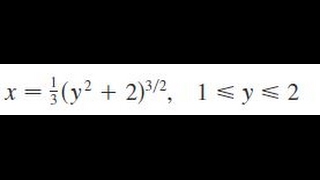



X 1 3 Y 2 2 3 2 1 Less Than Y Less Than 2 Youtube



Http Www Spsstavcb Cz Download2 578 2554 Cs Analytika Primka Pdf
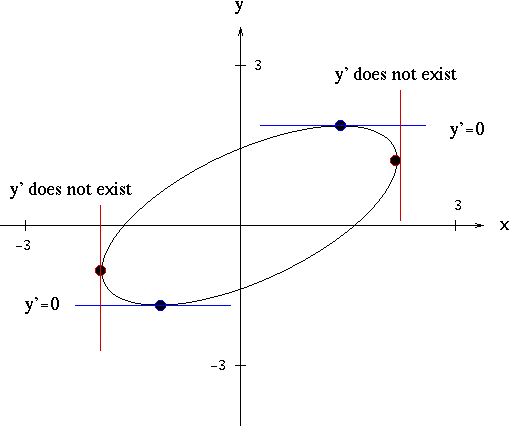



Solutions To Implicit Differentiation Problems




Ex 3 2 8 Find X If Y 3 2 1 4 2x Y 1 0 3 2
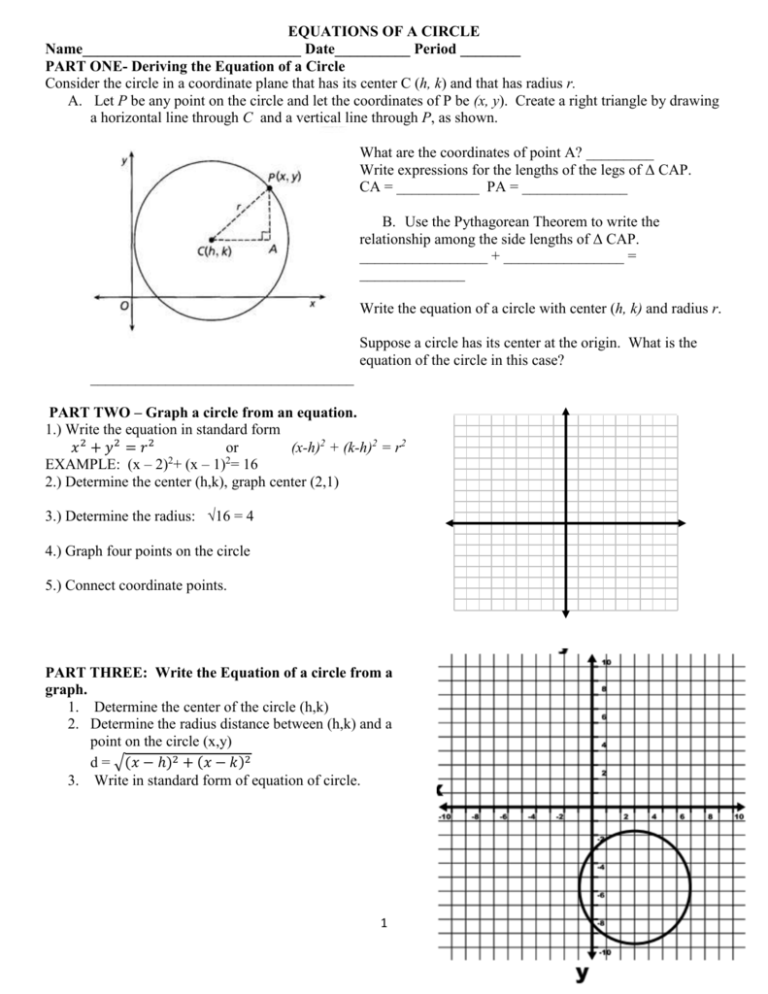



X 3 2 Y 1




X 2 2y 3 1 And X 3 Y 2 13 6 Solve Equal Brainly In




Engineering Mathematics Notes



How Do We Solve X 2 Y 2 10 1 X 1 Y 4 3 Quora
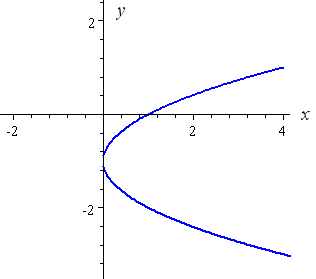



How To Draw Y 2 X 2 Interactive Mathematics
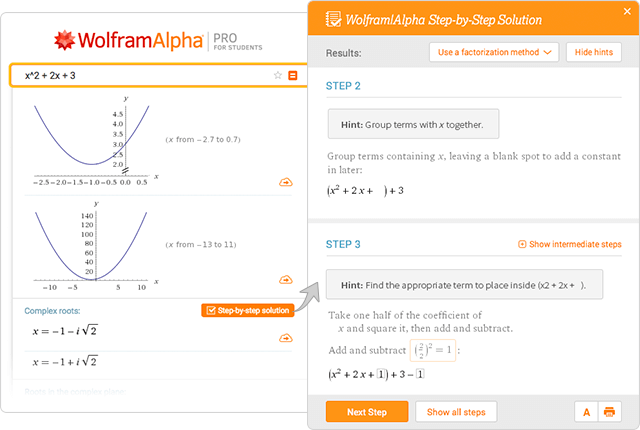



Wolfram Alpha Examples Step By Step Solutions




Problem Math 001 Pdf Trigonometric Functions Area
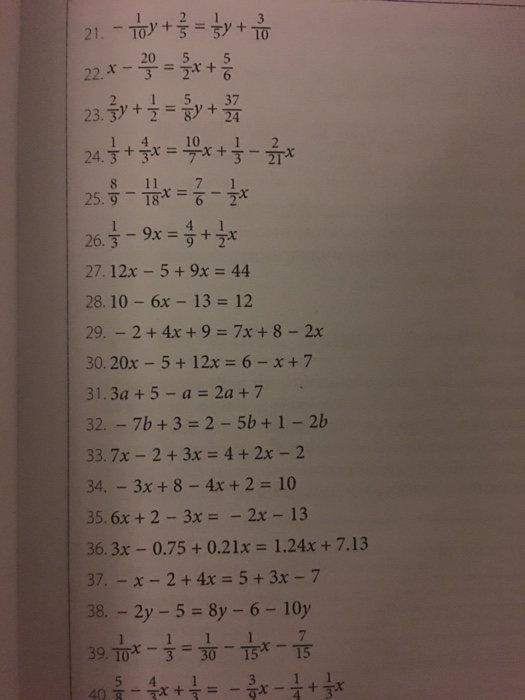



1 10 Y 2 5 1 5 Y 3 10 X 3 5 2 X 5 6 Chegg Com
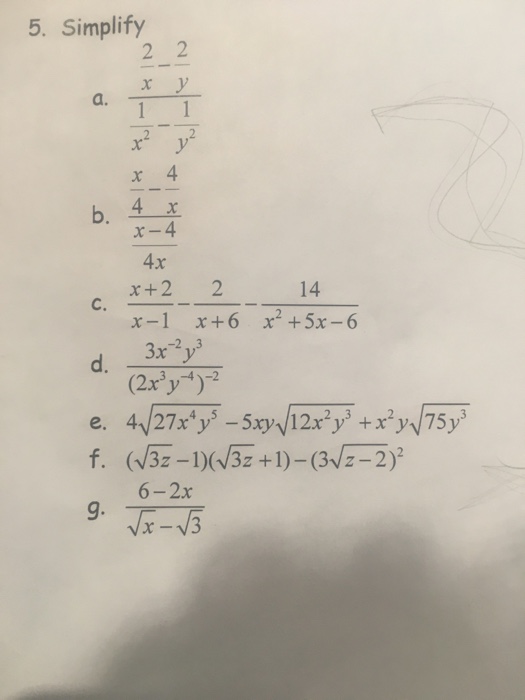



Simplify 2 X 2 Y 1 X 2 1 Y 2 X 4 4 X X 4 4x Chegg Com




If X 3 2 3 2 And Y 3 2 3 2 Then Find The Value Of X Y Please Answer Fast Brainly In




How To Imagine X 2 Y 2 1 0 In C 2 X Y Both Complex Mathematics Stack Exchange
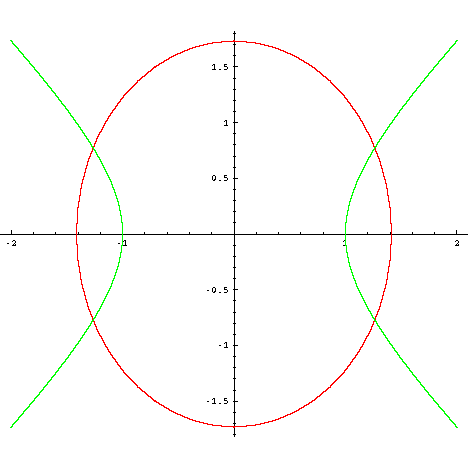



Graph Equations System Of Equations With Step By Step Math Problem Solver




Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples
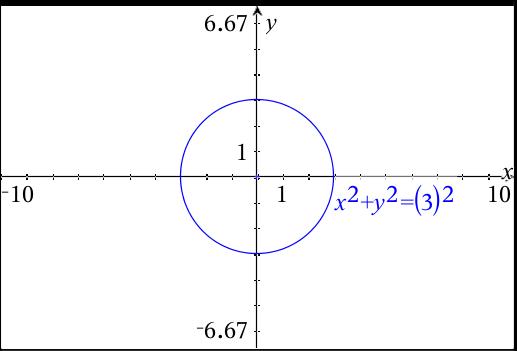



How Do You Graph X 2 Y 2 9 And What Are Its Lines Of Symmetry Socratic




Find The Derivative 1 Y X 3 3 X 2 Pi 2 2 Y Chegg Com




Vectors And The Geometry Of Space Monografias Com




If 2x 3 Y 2 1 6 0 And X 2 2y 3 3 Then



Show That The Lines X 1 2 Y 2 3 Z 3 4 And X 4 5 Y 1 2 Z Sarthaks Econnect Largest Online Education Community




Solution 1 Xsqrt X 2 Y 2 Dx Y 1 Sqrt X 2 Y 2 Dy 0 Is X Y 2 2 1 3 X 2 Y 2 3 2 C 0




Find The Asymptotes Of The Following Curves Y 3 X 2y 2x Y 2 2x 3 7xy 3y 2 2x 2 2x 2y 1 0




Plotting X 2 Y 2 1 3 X 2 Y 3 0 Mathematics Stack Exchange




Graphing Parabolas




If 2x Y 2 5 3x Y 1 3 2 X 2y 1 6 Then
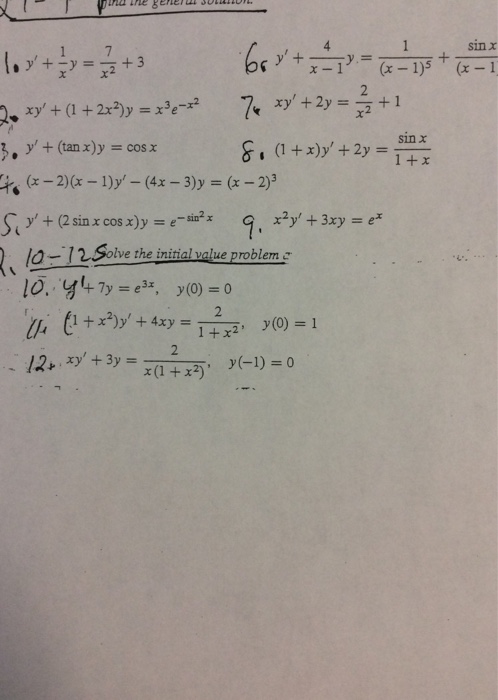



Y 1 X Y 7 X 2 3 Xy 1 2x 2 Y X 3 Chegg Com



What Is The Graph Of X 2 Y 3 X 2 2 1 Quora




These Are Answers1 K 32 X 4 Y 13 X 3 Y 04 P 9 7 Q 8 75 X 1 Y 16 X 2 Y 17 X 1 Y 18 Brainly In




How To Solve This Equation Math Begin Cases X 2 Y 11 Y 2 X 7 End Cases Math Quora



Solution 1 Graph X 3 1 8 Y 2 2 Write The Coordinates Of The Vertex And The Focus And The Equation Of The Directrix 2 Find All Solution To Each System Of Equations Algerbaiclly




If 2x 3y 2 3 4 0 And 3x 2y 2 2 1 5 Find X And Y Youtube




If X 2 1 Y 1 3 And Z 3 2 Find X 3 Y 3 Z 3 Xyz



What Is The Graph Of X 2 Y 3 X 2 2 1 Quora




X 2 Y 2 1then 4x 3 3x 2 3y 4y 3 2 Brainly In



0 件のコメント:
コメントを投稿