数学、特に初等解析学における(狭義の)一次関数(いちじかんすう、英 linear function )は、( 一変数 (英語版) の)一次多項式関数( firstdegree polynomial function )、つまり次数 1 の多項式が定める関数 ↦ をいう。( もしくは = と表記される)ここで、係数 a (≠ 0), b は x に依存しない定数一次反応速度式の性質 一次反応速度式を積分すると次のようになる。 = これは通常次のように指数減少関数として表記される。 = この式の異なる表記方法として以下のようなものがある。一次関数について,表,式,グラフを相互に関連付けて理解することができる。 二元一次方程式を関数を表す式とみることができる。 一次関数を用いて具体的な事象をとらえ説明することができる。 6 単元の評価規準 数学への 関心・意欲・態度
中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
エクセル 一次関数式
エクセル 一次関数式-比例も一次関数の一種ですが、比例の式に "定数項" が加わったものが一次関数です。 一次関数を表す式: 『y=ax b y = a x b 』数学、特に初等解析学における(狭義の)一次関数(いちじかんすう、英 linear function )は、( 一変数 (英語版) の)一次多項式関数( firstdegree polynomial function )、つまり次数 1 の多項式が定める関数 ↦ をいう。( もしくは = と表記される)ここで、係数 a (≠ 0), b は x に依存しない定数
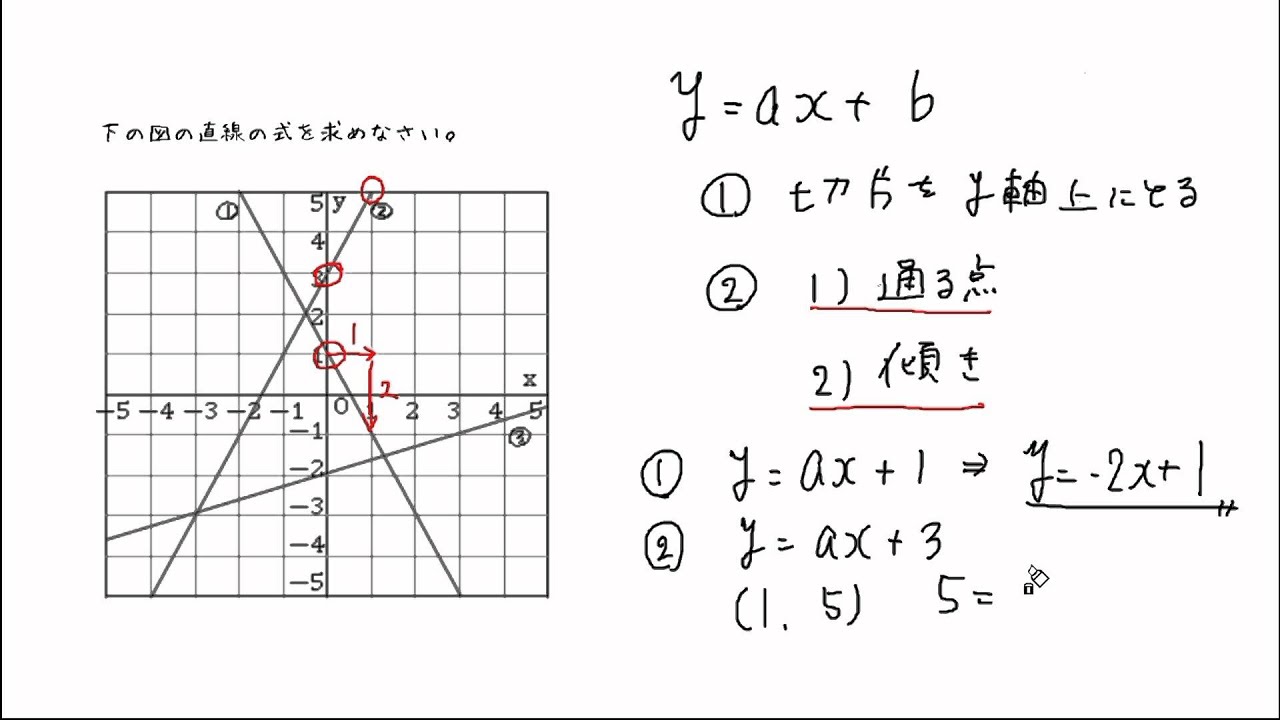



グラフから一次関数の式をもとめる Youtube
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru まず、「一次関数とは」についてですが、教科書にはこう書いてあります。 「yがxの関数で、yがxの一次式で表されるとき、yはxの一次関数である」 と定義してあります。 これで理解できる人は良いですがなかなか理解できないかな?2変数一次関数 数学についてのwebノート 定義: 2 変数 1 次関数 定義 ・「 2 変数関数 z = f ( x, y) が 1 次関数 である」とは、 定数 a, b, c を用いて、 2 変数関数 z = f ( x, y) を、 z = f ( x, y) = ax by c と表せることをいう。
2点を通る直線の方程式 切片を用いた直線の方程式 2直線の交点の座標 3点の座標で囲まれる三角形の面積 座標点で囲まれる多角形の面積 座標の回転 座標軸の回転 直交座標から極座標へ変換 極座標から直交座標へ変換まとめ 一次関数の式 は、 が に依る と、 が に依らない の足し合わせである。 のうち、 は傾き、 は切片 (\x=0\)のときの の値)を示す。 一次関数とは何か、一言で表すと、「比例関係常に変わらない値」で表される関数という事になります。 比例関係 前章・一次関数の式を求める ↓タップで拡大↓ 2点(あるいは2つの座標)が判明している場合の一次関数の式の求め方を、今回は扱っている。 \(x=〇のときy= \) という表現と \((x,y)\)を通る という表現が同じであるということは、前回も扱った。
中学数学で学習する一次関数の基本問題を全パターン解説します。 にゃんこ これらの練習問題は、中学2年生の数学の定期テスト対策にご利用ください。 一次関数の式や座標を求める練習問題:基本レベル 傾きがわかる 点(2,1)を通り、 傾き が-4のて,一次関数について理解するとともに,関数関係を見いだし表現し考察する能力を培 う。 ア 事象の中には一次関数としてとらえられるものがあることを知ること。 イ 一次関数について,表,式,グラフを相互に関連付けて理解すること。/1/7 2年一次関数総合問題Lv3 5 (2) 点Pはlとx軸の交点 (誤)→点Bはlとx軸の交点 (正) 3年方程式文章題 (割合2)3 (1)解答 2番目の式 yの係数 97 100 (誤)→ 93 100 (正) 7 3年2乗に比例する関数総合問題4 5問題 点A, P, Qを頂点とする (誤)→点D, P, Qを頂点とする




1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場



一次関数とは グラフの書き方や一次関数の利用問題の解き方 受験辞典
中2数学「一次関数の式を求めること(傾きと1点の座標がわかるとき)の問題」です。1次関数y=axbにおいて、 aの値がわかるとき → 傾き、変化の割合、平行な直線がわかっている場合 bの値がわかるとき → 切片がわかっている場合以上がウ.身のまわりの事象の中から一次関数の関係を見出すことができる。 エ.式からグラフをかくことができる。 オ.一次関数の式から傾きと切片がわかる。 実態調査より数学の学習が楽しいと約9割の生徒が思っていることがわかった。しかしながら,数学の次の場合について, y を x の式で表し、一次関数であるものには 一次関数でないものには×をつけましょう。 (1)水がℓ入っている水そうに,毎分ℓの割合で x 分間水を入れる
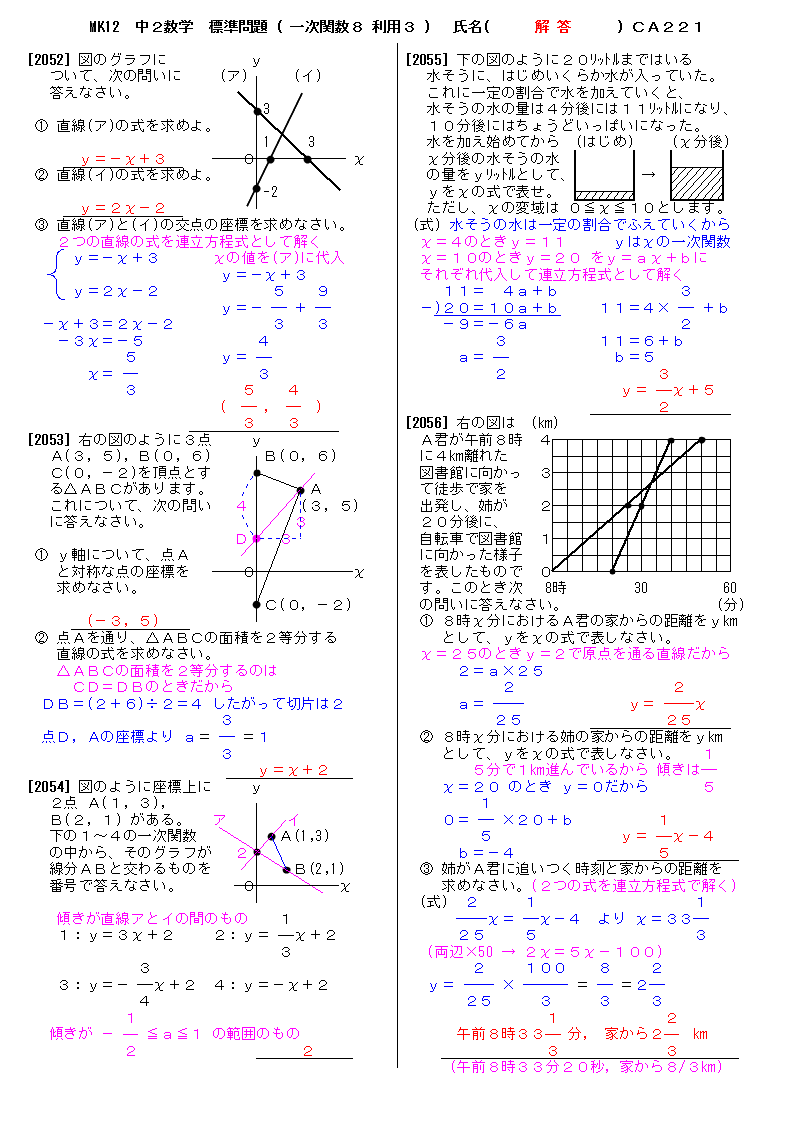



無料 中2数学 標準問題 解答プリント 221 一次関数8 利用3




数学 中2 37 一次関数の交点をだす 応用編 Youtube
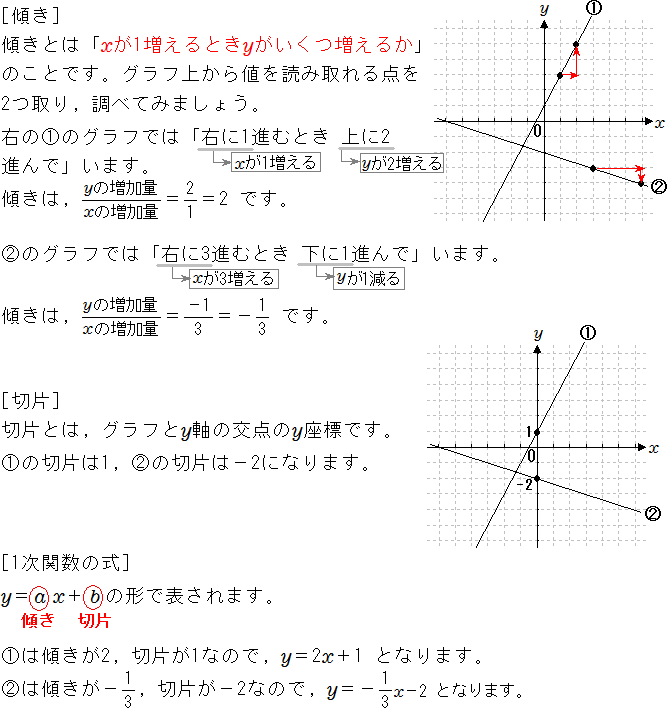
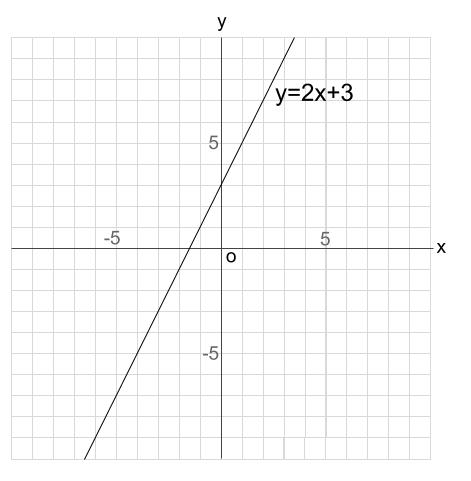
直線の方程式(一次関数)はy=ax+b (a,bは定数)で表わされます。 (※y軸に平行なものを除く。) 2点を通る直線の方程式を求めるには,2点のx,y座標を直線の方程式に代入して,定数a,bの連立方程式を解きます。 例題1この基本式のうち、 a と b は定数(ていすう)と言い値が変わりません。 また x と y は変数(へんすう)と言い、 x の値が変われば y の値も変わっていくものです。 一次関数はグラフを使って表すことができます。例えば y =2 x 1 という一次関数は以下のようなグラフになります。1 特殊な比例が一次関数 11 一次関数には傾きと切片があり、 y = a x b の式になる 2 一次関数のグラフの書き方 21 変化の割合:分数を含むグラフの書き方




Excel エクセルで一次関数を計算し グラフを作る方法 一次関数の解を求める方法



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
(1) グラフが次のようになる一次関数の式を,それぞれ求めなさい。 ① 傾きが4で,切片が-3の直線 ② 2点(-6,1),(2,-3)を通る直線 (2) 下の表は,ある一次関数について,x の値とy の値の関係を示したものです。 y をx の式で表しなさい。 1つ目は、x=0のときはy=0になること。 2つ目は、 xの値を2倍・3倍・4倍すると、それに対応するyの値も2倍・3倍・4倍する ことです。第6節 1次関数と方程式 ☆ 1次関数は式を用いて表されました。同じように式を用いるものとして方程式を学習し ました。ここでは関数と方程式の関わりについて調べていきましょう。 (1)2元1次方程式 2元1次方程式 2xy=7 で、xが次の値のときにyの値を求め
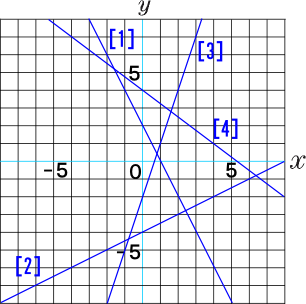



中学2年数学練習問題 一次関数の直線の式 傾き 切片 を求める問題




一次関数の直線の式についてです グラフから読み取るやつです 全くわかりません Clear
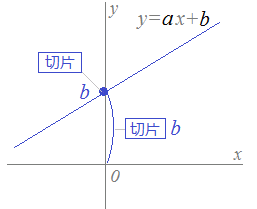
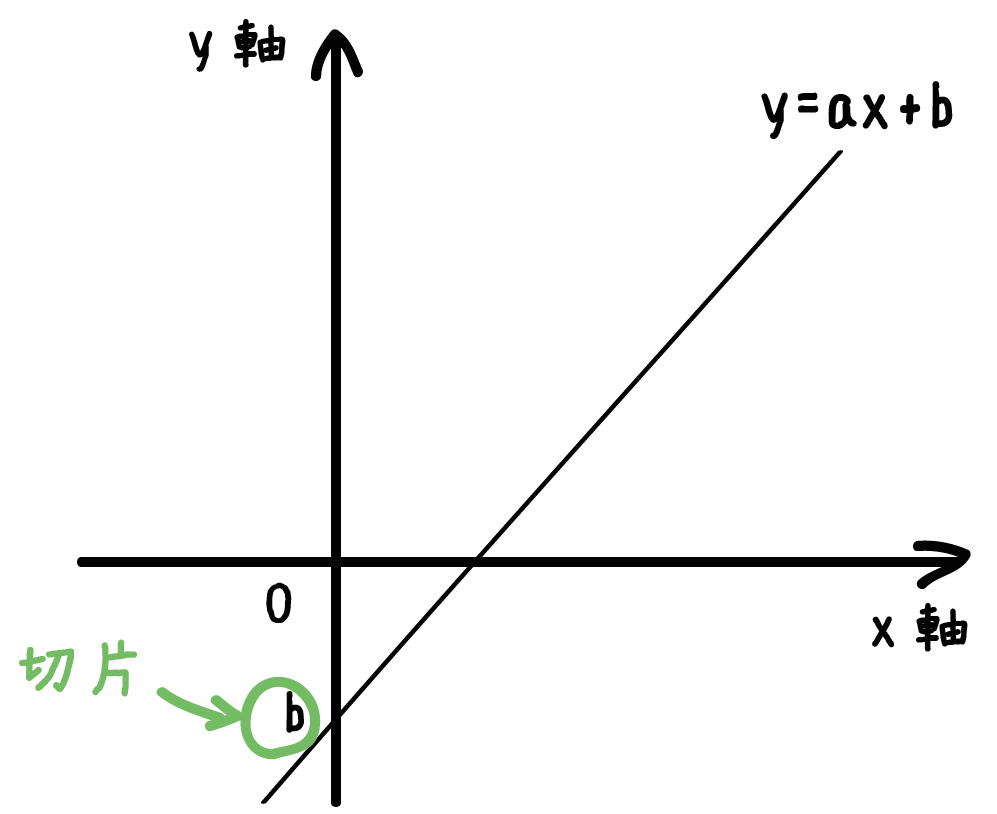
イ 一次関数について,表,式,グラフを相互に関連付けて理解すること。 ウ 二元一次方程式を関数を表す式とみること。 エ 一次関数を用いて具体的な事象をとらえ説明すること。 学習指導要領の内容項目C関数(1)一次関数の式に \(x=0\) を代入して計算していきましょう。 すると、交点の\(y\)座標を求めることができるので\(y\)軸との交点は $$(0, y座標)$$ とすることができます。 また、一次関数の式 \(y=axb\) の\(b\)部分を見ることですぐに求めることもできます。 一次関数の式にでてくる\(a\)のことを 傾き(かたむき) \(b\)のことを 切片(せっぺん) といいます。 あとで一次関数のグラフや式をつくっていくときに、とっても大切な言葉になるから覚えておきましょう!
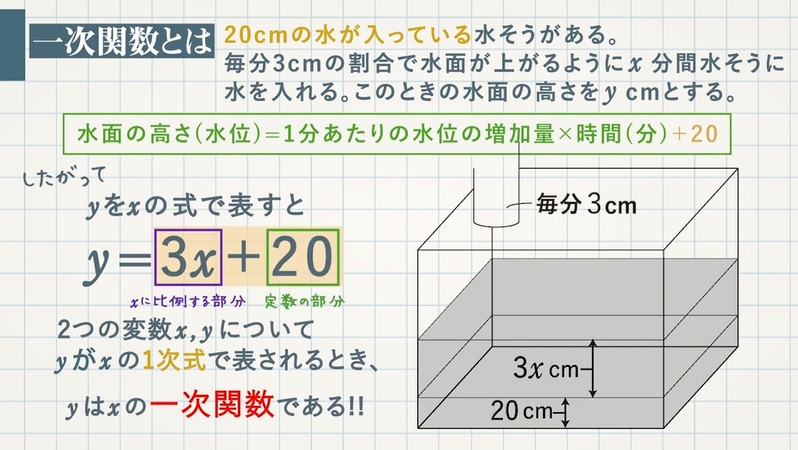



一次関数とは Yがxの1次式で表される関数 教遊者
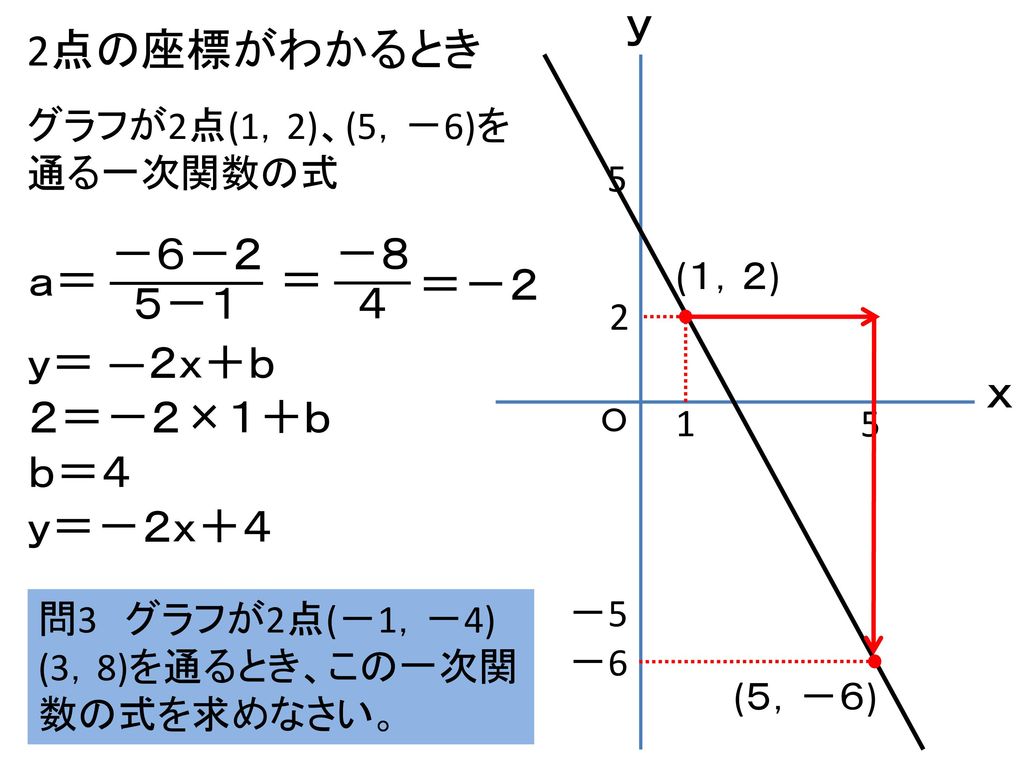



一次関数のグラフ 式を求めること 本時の流れ ねらい グラフや座標など与えられた条件をもとに一次 関数の式を求める Ppt Download
この頁の目標 1次関数のグラフを見て,方程式が答えられるようにする. i 直線のグラフから「切片」と「傾き」を読み取れるようにする. ii 直線のグラフから1次関数の方程式を答えられるようにする. iii 傾きが分数になるときでも,直線のグラフから1次関数の方程式を答えられるようLINE Pocket 今回は中2で学習する 『一次関数』の単元から 直線の式の求め方について解説していくよ! ここでは、いろんなパターンの問題が出題されるので パターン別に例題を使って解説していA 、 b を 定数 とするとき y =a x +b (a≠0)で表される 関数 をいう。 とくに、定数bが0であれば、yはxに 比例 (正比例)する。 定数項bは、xの 値 が0のときのyの値を表す。




中学2年の数学 動画 一次関数の式をもとめる 基本編の問題 19ch
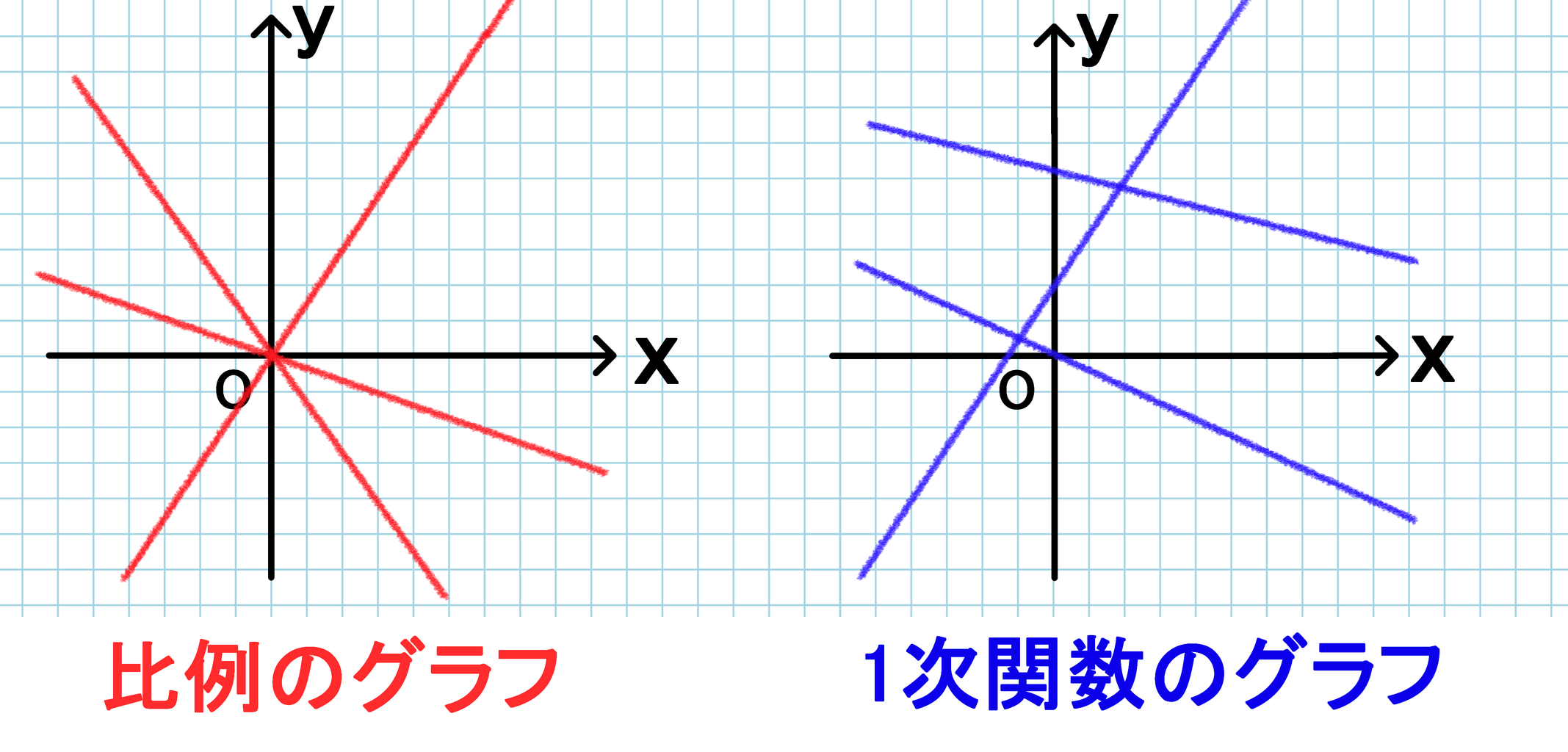



1次関数と比例の違いとは バカでもわかる 中学数学
傾きと1点の座標がわかる場合 傾き= a = y = a x b に代入する 点の座標の x と y を代入して b を求める 一次関数の直線の式がわかる3つの求め方 まず、直線の式が計算できるケースを確認しよう。 つぎの4つの要素のうち、2つの値がわかっているときに式が求められるんだ。 傾き(変化の割合) 切片 直線が通る座標1 直線が通る座標2 たとえば、傾きと考 一次関数のグラフを基にグラフのもつ特徴を考察す ることができる。 技 一次関数の表や式,グラフをかくことができる曇 技 変域をもつ一次関数のグラフをかくことがで去る‐ 知 変化の様子,グラフの形,切片,傾きなどの意味を 理解している。



1




1次関数 1次関数の式の求め方 中学数学 定期テスト対策サイト




中学校数学 2年生 数量 一次関数 Wikibooks



なぜ弟の計算では Y Ax B の公式を使わなくて 兄には Y Ax B の公 Yahoo 知恵袋




一次関数 表から式を求めるやり方についてイチから解説 Youtube
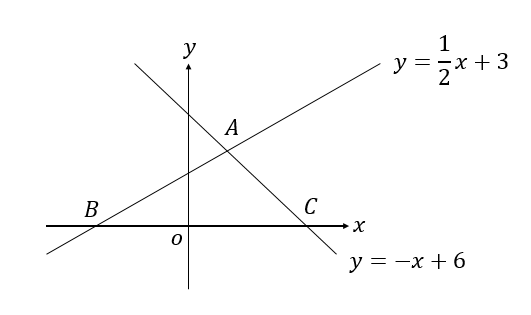



一次関数 面積を求めるやり方は 2等分の式はなに 数スタ




中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
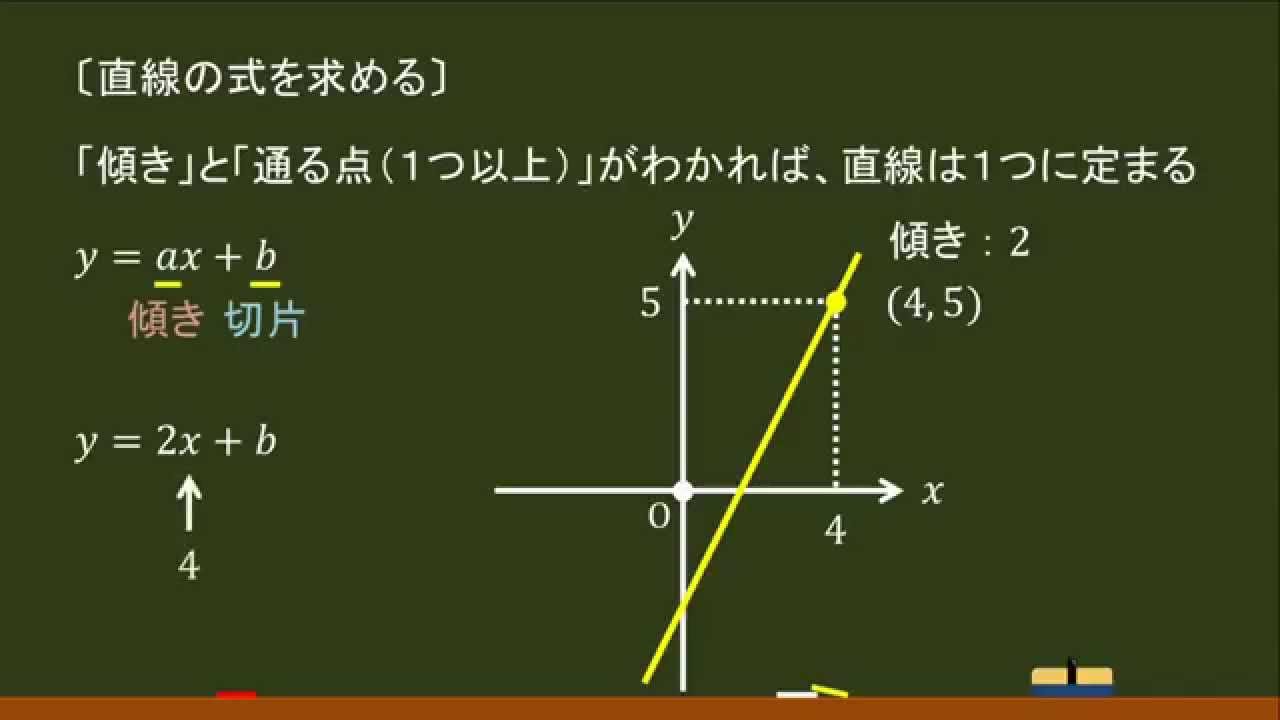



中2数学 1次関数 直線の式を求める 傾きと通る1点から オンライン無料塾 ターンナップ Youtube
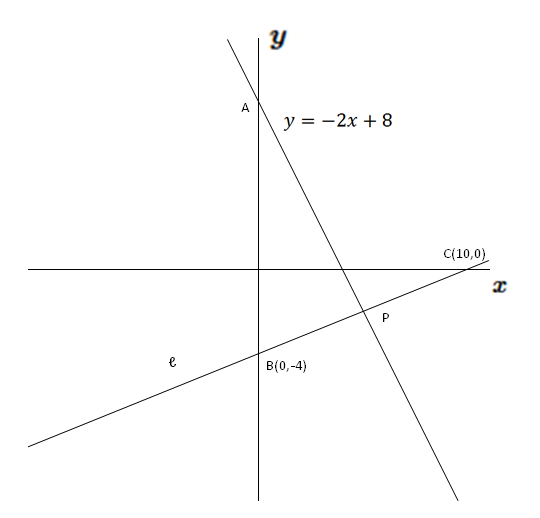



一次関数の応用 6 ネット塾




中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




一次関数のグラフ 式を求めること 本時の流れ ねらい グラフや座標など与えられた条件をもとに一次 関数の式を求める Ppt Download



1次関数 グラフから直線の式を求める 勉強ナビゲーター
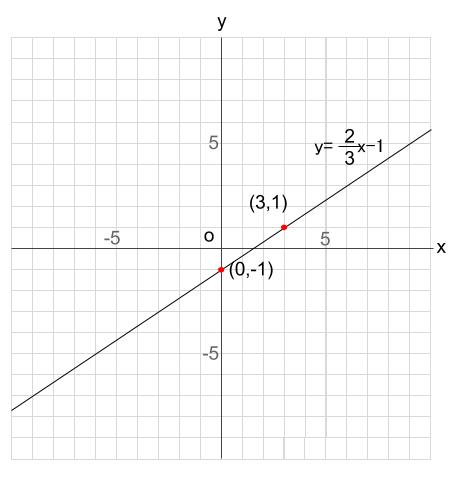



中学数学 1次関数 式からグラフへ 中学数学の無料オンライン学習サイトchu Su



1次関数 グラフ 直線の方程式
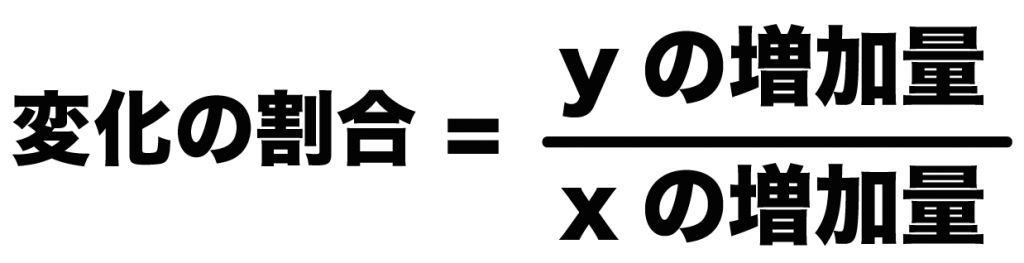



1次関数の公式 変化の割合の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



一次関数 Wikipedia




無料 中2数学 基本解説 問題プリント 217 一次関数4 式の求め方



1次関数 1次関数のグラフの読み取りの基礎 中学数学 定期テスト対策サイト




1次関数3 1次関数のグラフの交点と連立方程式の解 身勝手な主張




1次関数 2点を通る直線の式の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
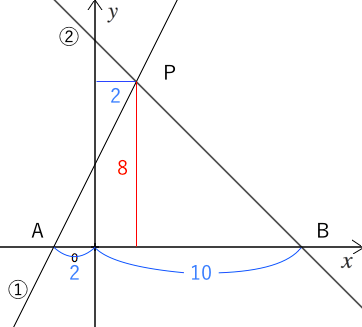



一次関数の利用 2直線が交わる 苦手な数学を簡単に




一次関数 グラフから式を求める方法について徹底解説 数スタ




一次関数 変域問題の解き方 変域から式を求める方法とは 数スタ




一次関数とは Yがxの1次式で表される関数 教遊者



超速まとめ 一次関数 一次関数の式 変化の割合 グラフ 二元一次方程式 Shun Ei Note
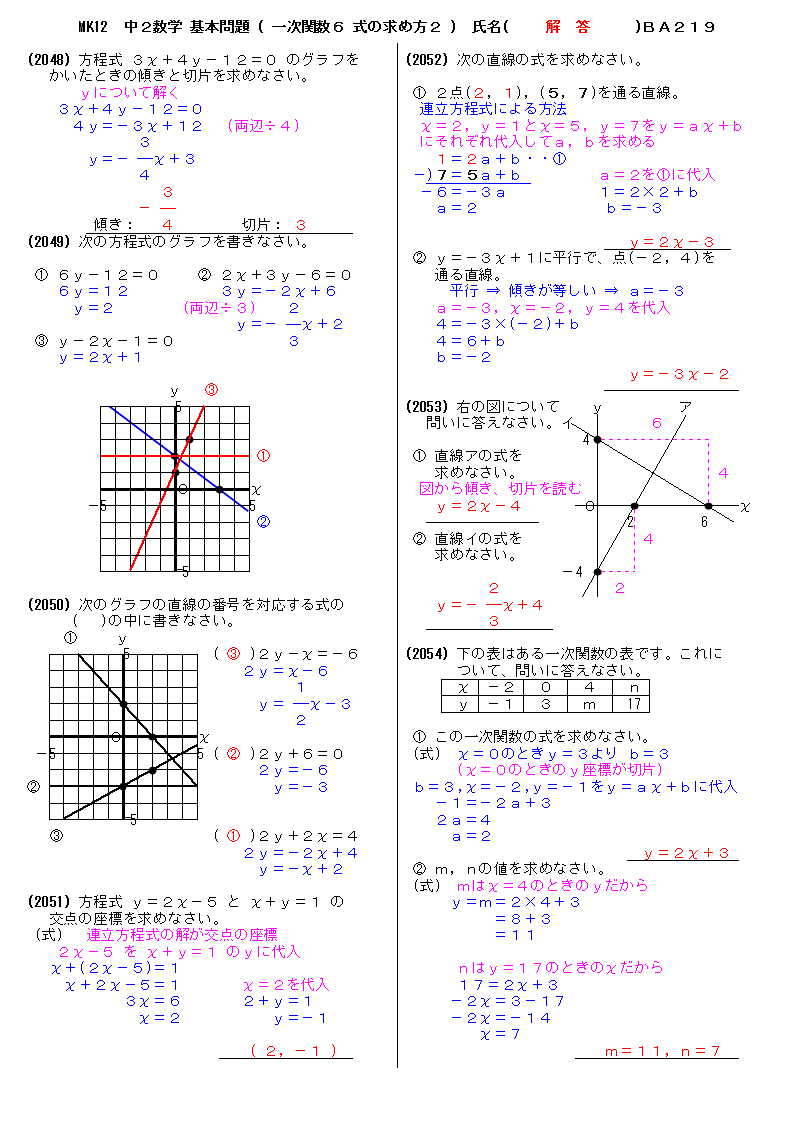



無料 中2数学 基本問題 解答プリント 219 一次関数6 式の求め方2




数学 中2 32 一次関数の式をもとめる 基本編 Youtube
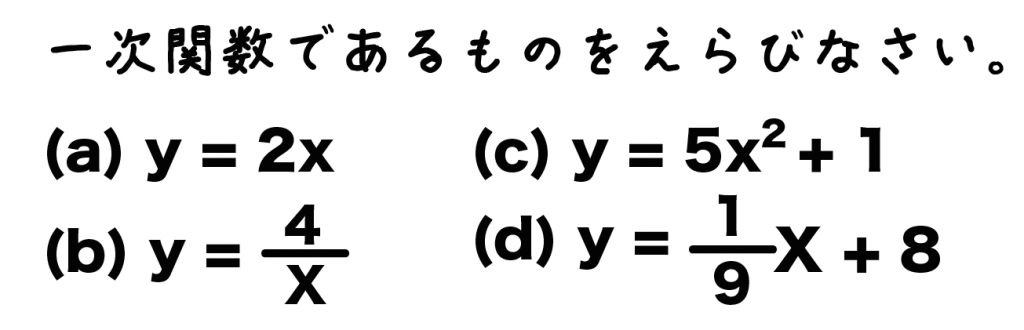



中学数学 一次関数とはなんだろう Qikeru 学びを楽しくわかりやすく




中学数学 一次関数




一次関数のグラフの利用1 無料で使える中学学習プリント




中学2年の数学 動画 一次関数の式をもとめる 練習編の問題 19ch




グラフから一次関数の式をもとめる Youtube




数学 中2 33 一次関数の式をもとめる 練習編 Youtube



3




一次関数とは 式とグラフの解説 数学fun




かずお式中学数学ノート9 中2 一次関数 Amazon Com Books




切片とは 超簡単 切片を一瞬で求める方法 傾きとの違い 高校生向け受験応援メディア 受験のミカタ
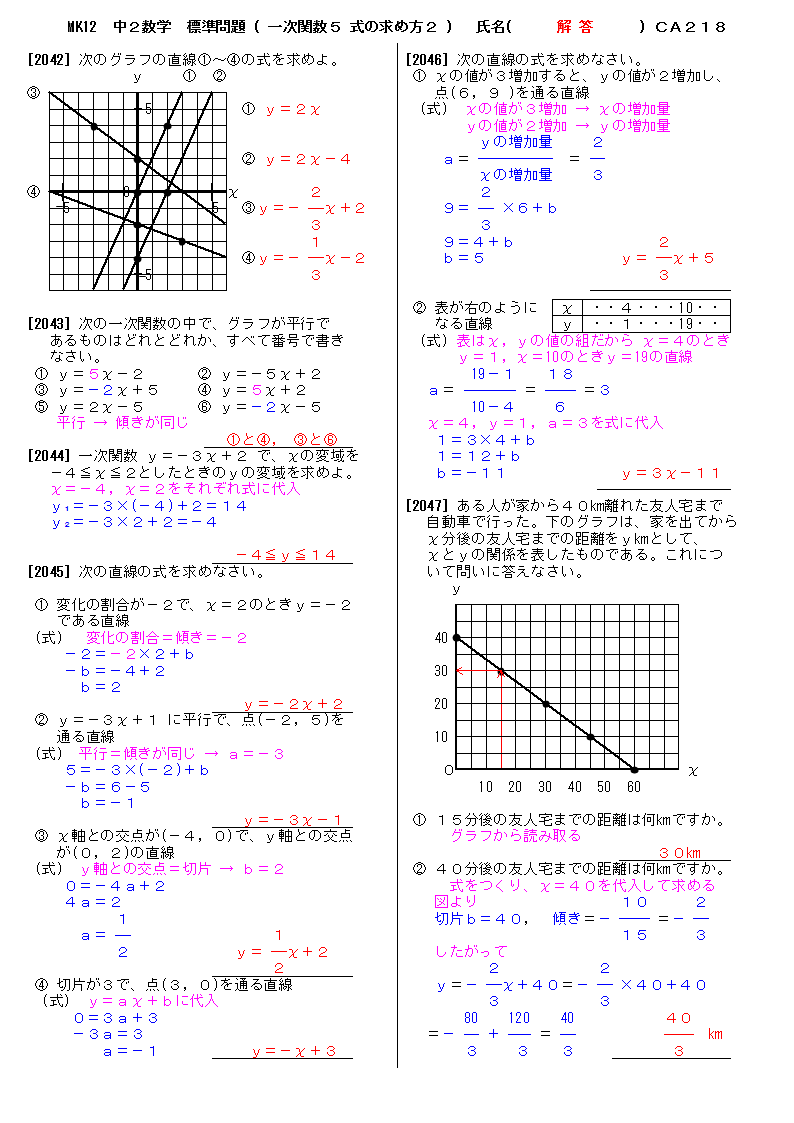



無料 中2数学 標準問題 解答プリント 218 一次関数5 式の求め方2




変化の割合の求め方 一次関数と二次関数の変化の割合を求めよう 中学や高校の数学の計算問題




一次関数とは Yがxの1次式で表される関数 教遊者




一次関数 直線の式 変化の割合 8種類 問題解答自動作成 授業で使える教材倉庫
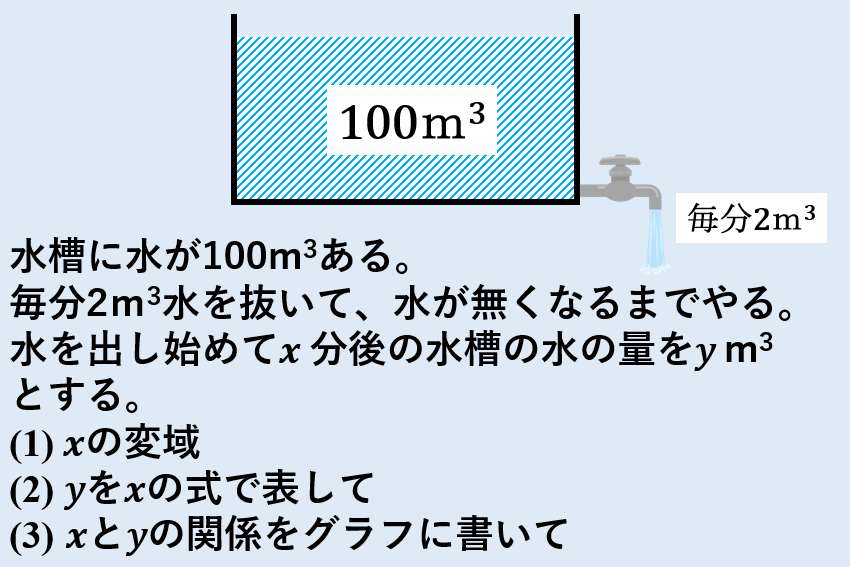



中2数学 一次関数の利用 水槽から水を抜く 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
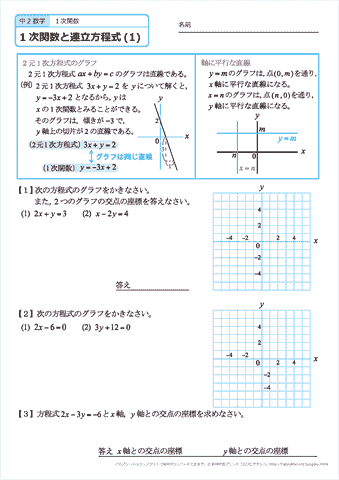



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中2数学 1次関数 式の求め方 Youtube




2点から一次関数の式を求める チーム エン




一次関数 直線の式の求め方 Youtube




一次関数 2点を通る直線の式の求め方をイチから解説 Youtube




たけのこ塾 Twitterissa 中2数学 今回は 一次関数のグラフ の問題を作成しました 一次関数の式 Y Ax Bの 傾きa からグラフの傾き具合を 切片b からグラフとy軸との交点のy座標を読み取ります 詳しくは画像の解説をご覧下さい 勉強垢 中2 数学




数学 中2 36 一次関数の交点をだす 基本編 Youtube
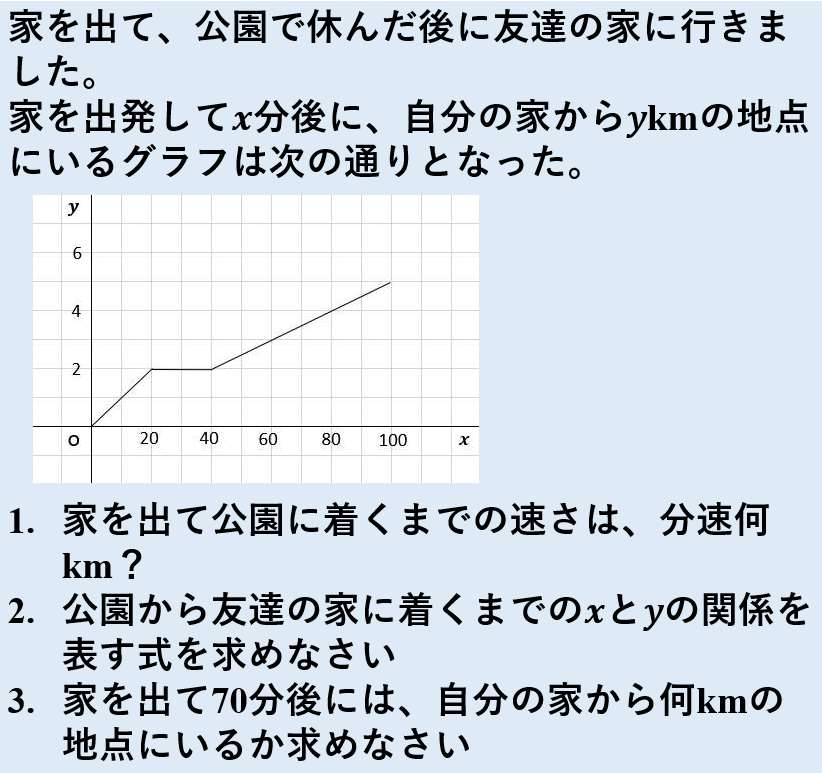



中2数学 一次関数の利用 文章題 歩く距離と時速のグラフ問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
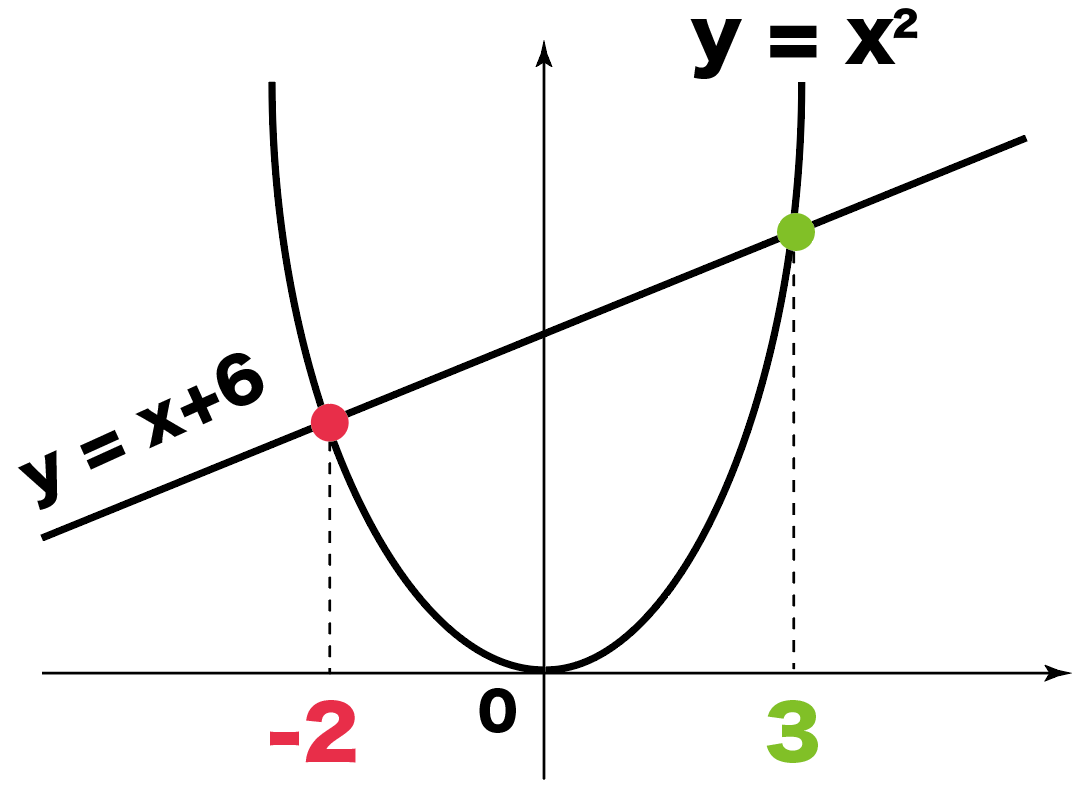



一次関数と二次関数の交点の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




1次関数のグラフの応用 3種類の交点とグラフ上の面積 教遊者




数学 中2 42 一次関数の利用 一人のみはじ編 Youtube
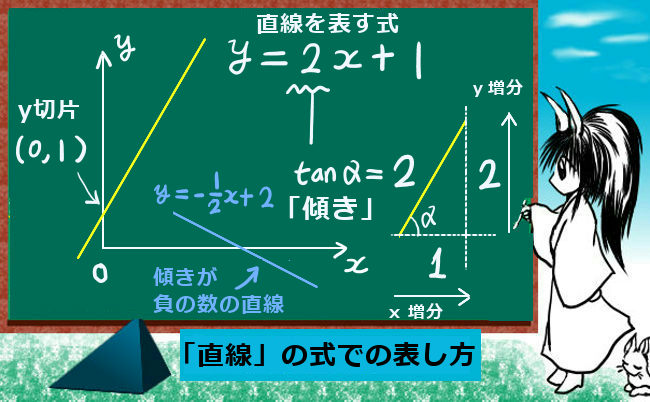



直交座標上の直線 理数系無料オンライン学習 Kori




中2 中2数学 一次関数 1 中学生 数学のノート Clear
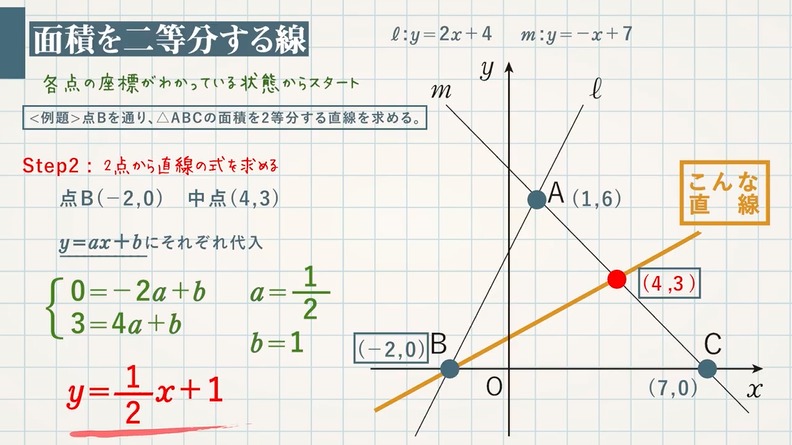



1次関数のグラフの応用 面積を二等分する線 面積が等しくなる点 教遊者
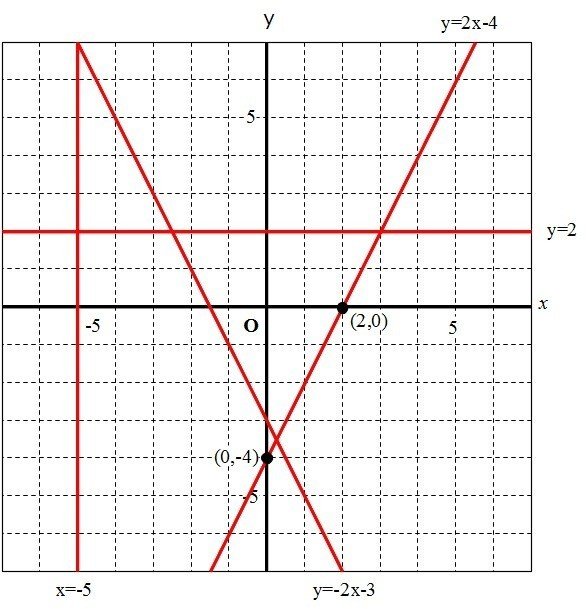



超速まとめ 一次関数 一次関数の式 変化の割合 グラフ 二元一次方程式 Shun Ei Note
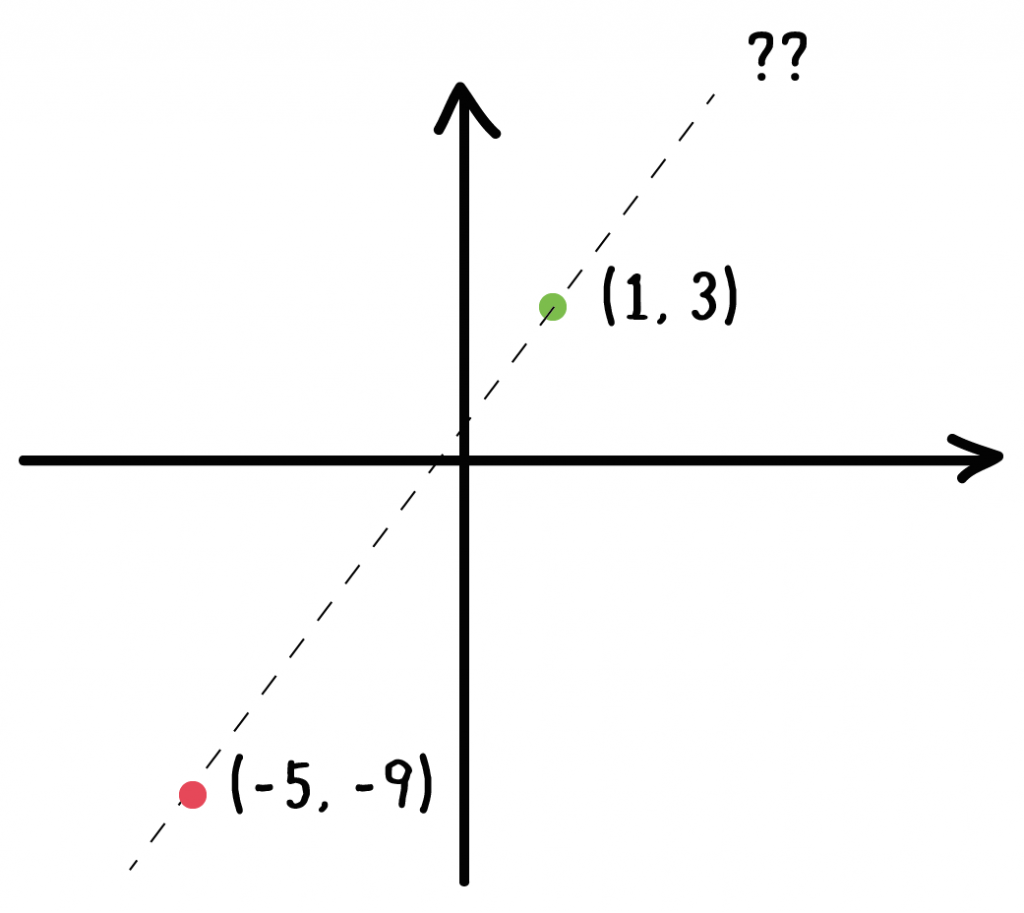



一次関数 直線の式がわかる4つの求め方 Qikeru 学びを楽しくわかりやすく




中学数学 一次関数とはなんだろう Qikeru 学びを楽しくわかりやすく



1



中2の数学 をバッチリ攻略 連立方程式や一次関数を解説 家庭教師ジャニアス



一次関数の要点まとめ




中2 数学 3 一次関数 Youtube 数学 プリントアウト




世界一わかりやすい数学問題集中2 3章 一次関数




3分で分かる 一次関数の意味 用語 グラフの書き方をわかりやすく 合格サプリ



中学数学 1次関数のグラフ 中学数学の無料オンライン学習サイトchu Su



中2数学 一次関数の切片を求める2つの方法 Qikeru 学びを楽しくわかりやすく




一次関数 連立方程式とグラフの関係 苦手な数学を簡単に




中学2年生 一次関数の式を求めよう 学童cafe チャイルドスペース




中2数学 直線の式の求め方3 2点の座標がヒント 練習編 映像授業のtry It トライイット




一次関数の問題の解き方 7パターン 数学fun




一次関数 式の求め方をパターン別に問題解説 数スタ
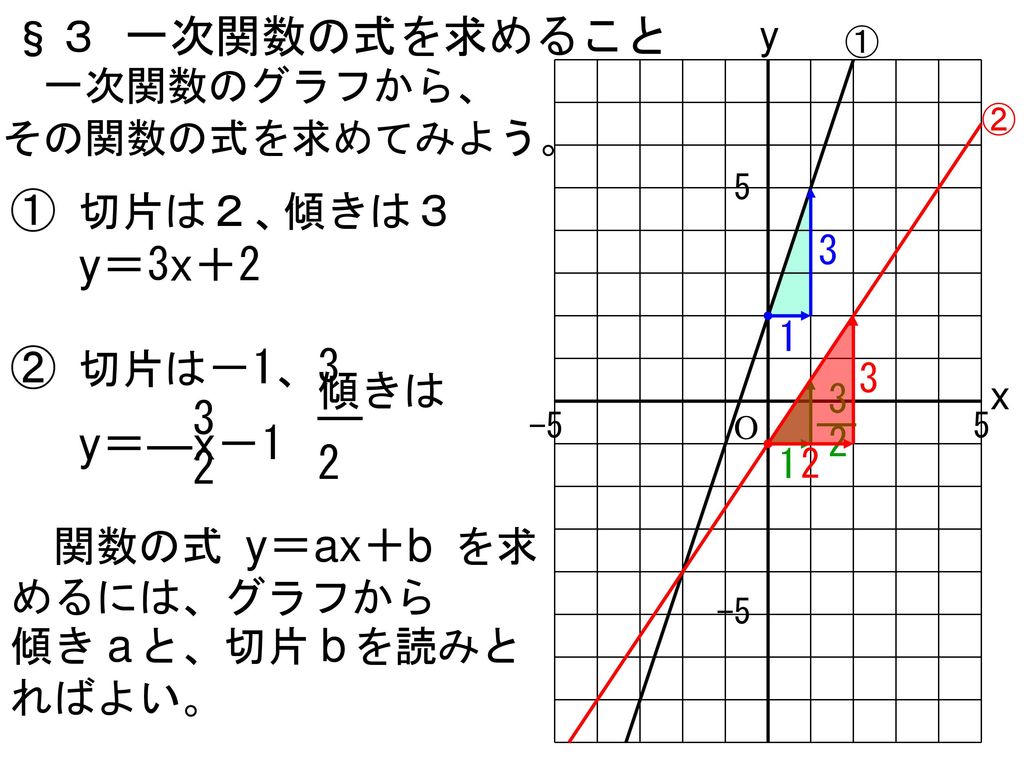



3 一次関数 1章 一次関数とグラフ 3 一次関数の式を求めること 3時間 Ppt Download
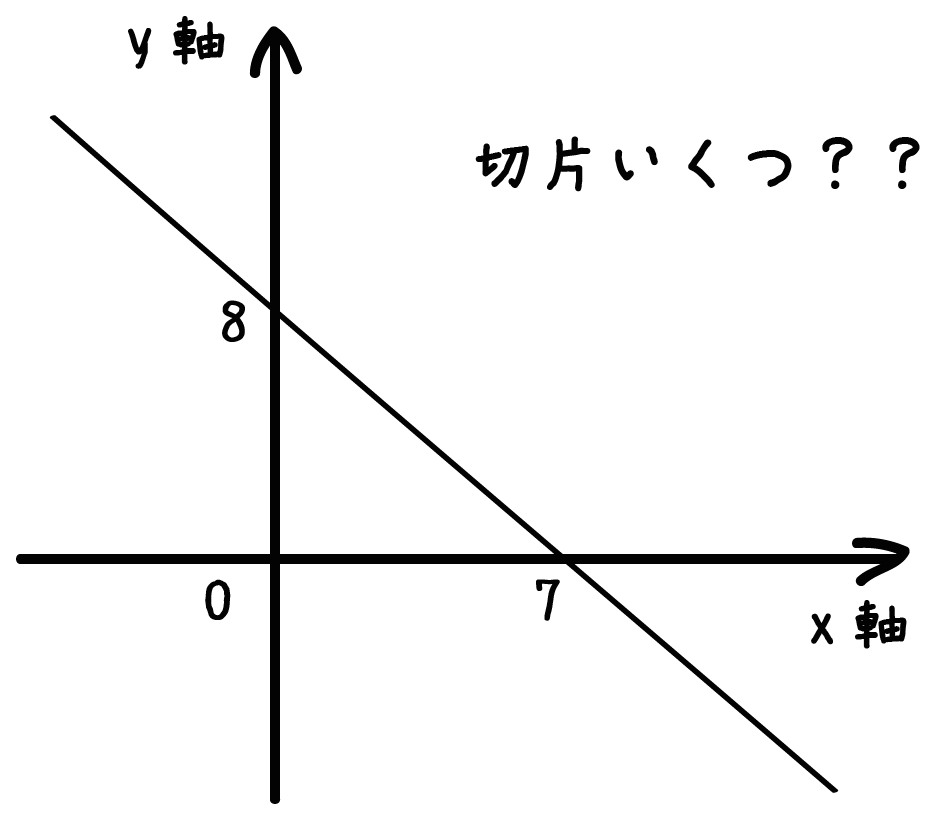



中2数学 一次関数の切片を求める2つの方法 Qikeru 学びを楽しくわかりやすく




高校数 関数 1次関数の方程式 定義域と値域から求める オンライン無料塾 ターンナップ Youtube
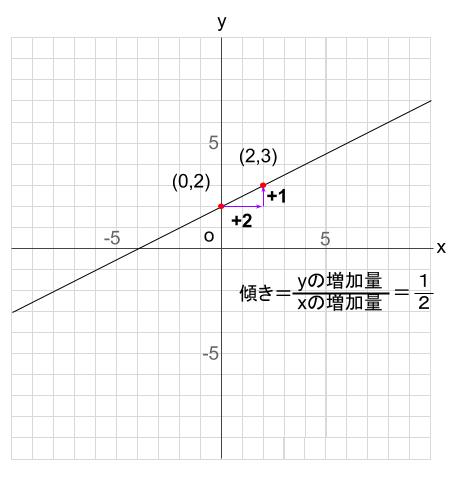



中学数学 1次関数 グラフの読み取り 中学数学の無料オンライン学習サイトchu Su




一次関数の式を求める チーム エン
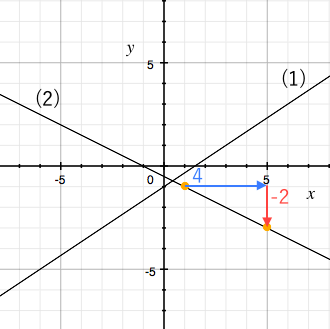



一次関数 グラフから関数の式を答える 苦手な数学を簡単に




中学校数学 2年生 数量 一次関数 Wikibooks




1 1 3 2 5 X2y3 2 3 Descubre Como Resolverlo En Qanda




一次関数の式を決定1 無料で使える中学学習プリント




切片が分からないときの一次関数の式の求め方 チーム エン
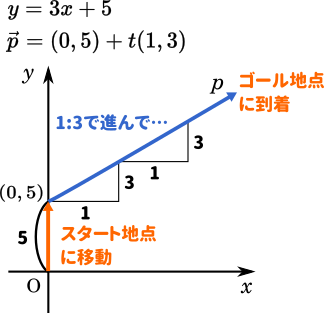



ベクトル方程式と媒介変数表示の仕組み やってることは一次関数と同じ Mm参考書
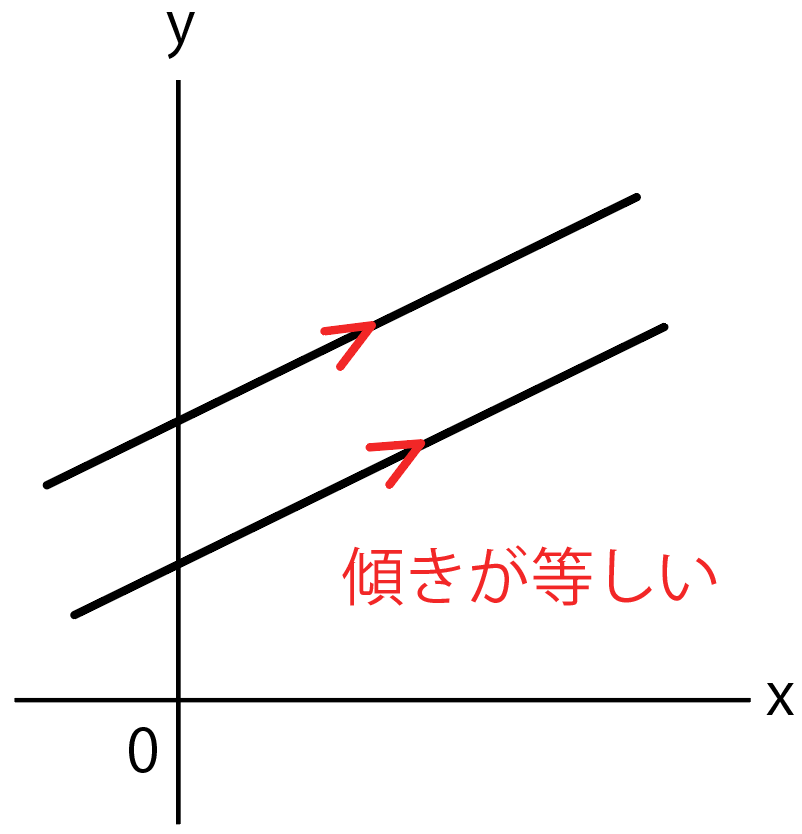



一次関数 テストに出やすい 平行な直線の式の求め方 Qikeru 学びを楽しくわかりやすく



1



U9j580gf8iba369ji2w Xyz P 762




一次関数の問題です 途中式を教えてください お願いします Clear




一次関数はこれで完璧 グラフの書き方と変化の割合の求め方



1次関数 直線の式 中学から数学だいすき




一次関数を子供に教える




次の条件を満たす一次関数の式を求めなさい Clear



0 件のコメント:
コメントを投稿