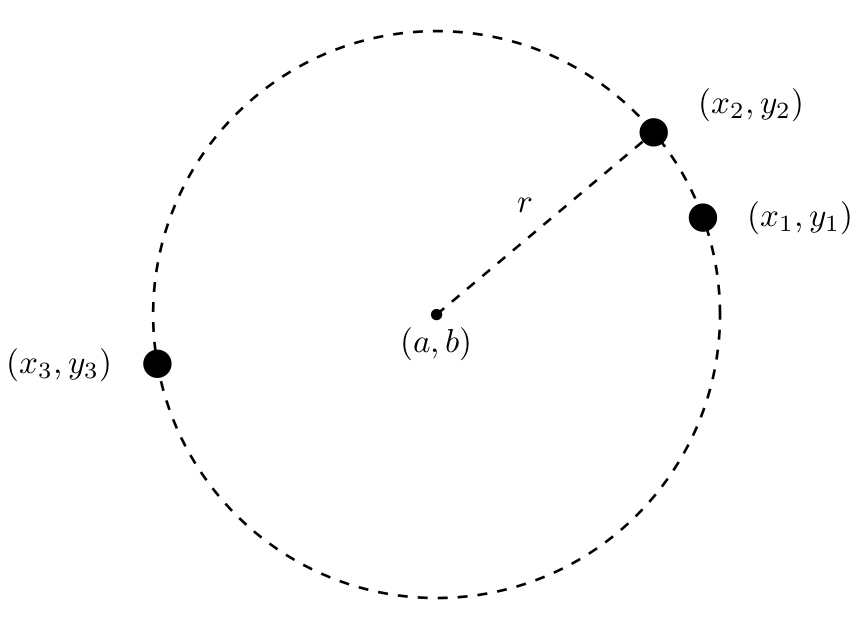
3点を通る円の中心と半径 Notes Jp
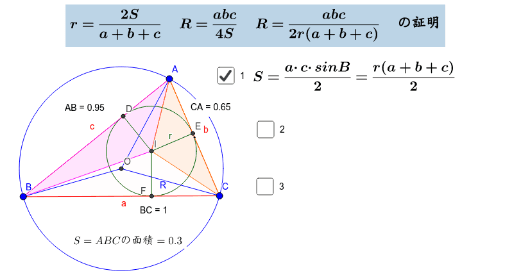
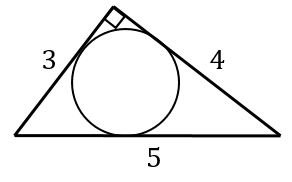
内接円の半径の計算方法 内接円 とは,三角形の3つの辺全てに接する円のこと。 内接円の半径は, S=\dfrac {r} {2} (abc) S = 2r(a b c) という公式を使って計算できる。 三角形の内接円について解説します。 前半では,内接円の半径を計算する方法を解説し 円っぽい式から中心・半径を求める 円の式は \( x^2Ax y^2 By = C \) の形で書けますが 逆にこの形の式は円かと言われるとそうとは限りません。 そこでこの形の式が与えられたときこれが円の式かどうか,円ならば中心と半径を求めてみたいと思います。
円 半径 求め方 座標
円 半径 求め方 座標-円周とは円の周りの長さです。 円周は「直径×円周率」で算定します。 直径=2×半径(半径=直径÷2)なので「円周=直径×円周率=2×半径×円周率」となります。 さらに円周率≒314なので、円周L=2πr=628rですね。 もっと簡単に計算する場合、円周率円の面積から半径 110 /19件 表示件数 1 1753 40歳代 / 自営業 / 非常に役に立った / 使用目的 スピーカー設計 ご意見・ご感想 エンクロージャーに複数の円形ダクトを入れる際の面積から逆算して直径を割り出すために
円周の求め方と円の面積について アタリマエ
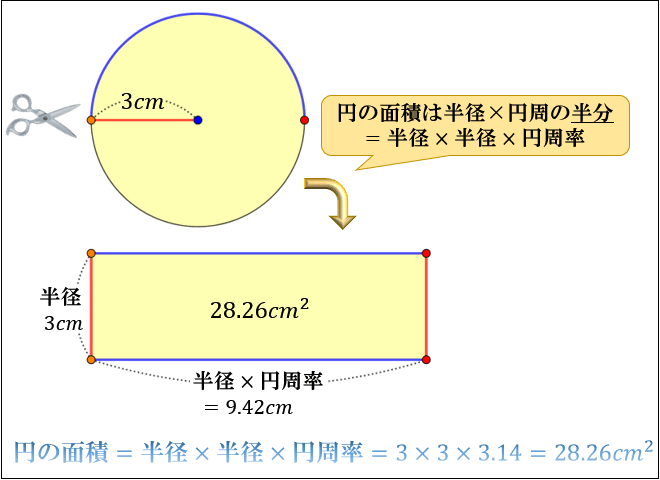
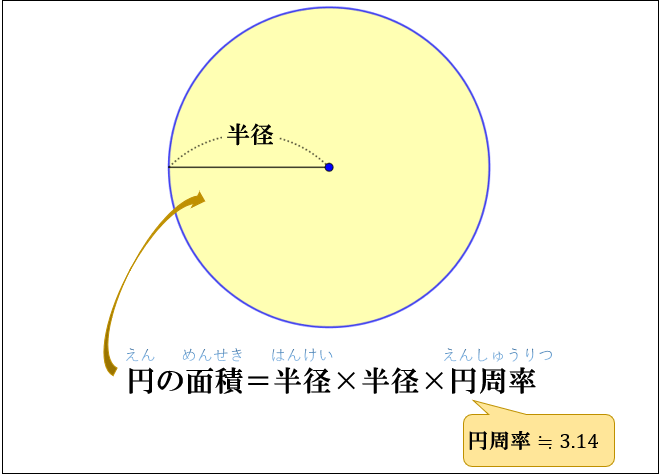
例題 上節でみたように,$2$ 円の位置関係を調べるには,$2$ つの円の半径と,中心間の距離を調べればよいのでした.円の方程式からその中心の座標と半径を求める方法は前記事 →円の方程式の表し方 で紹介しています.これらの知識を用いて,実際にいくつかの例題を解いてみましょう. 円周の長さから円の半径と直径を計算する|オンライン電卓 何日後と何日目と何日前の違いと数え方:何日後は足し算、何日前は引き算で計算する 0 Irohabook @go 10 June 19 円周の長さから円の半径と直径を計算する|オンライン電卓 0 8076 中学数学 円の面積の求め方 円の面積を求めるときは 円の面積 = 半径 × 半径 × 円周率 という公式を使います。 たとえば、半径が 3 c m の円の面積は 半径 半径 円周率 半 径 × 半 径 × 円 周 率 = 3 × 3 × 314 = 26 c m 2 と求めることができます。 Tooda Yuuto 「なんで
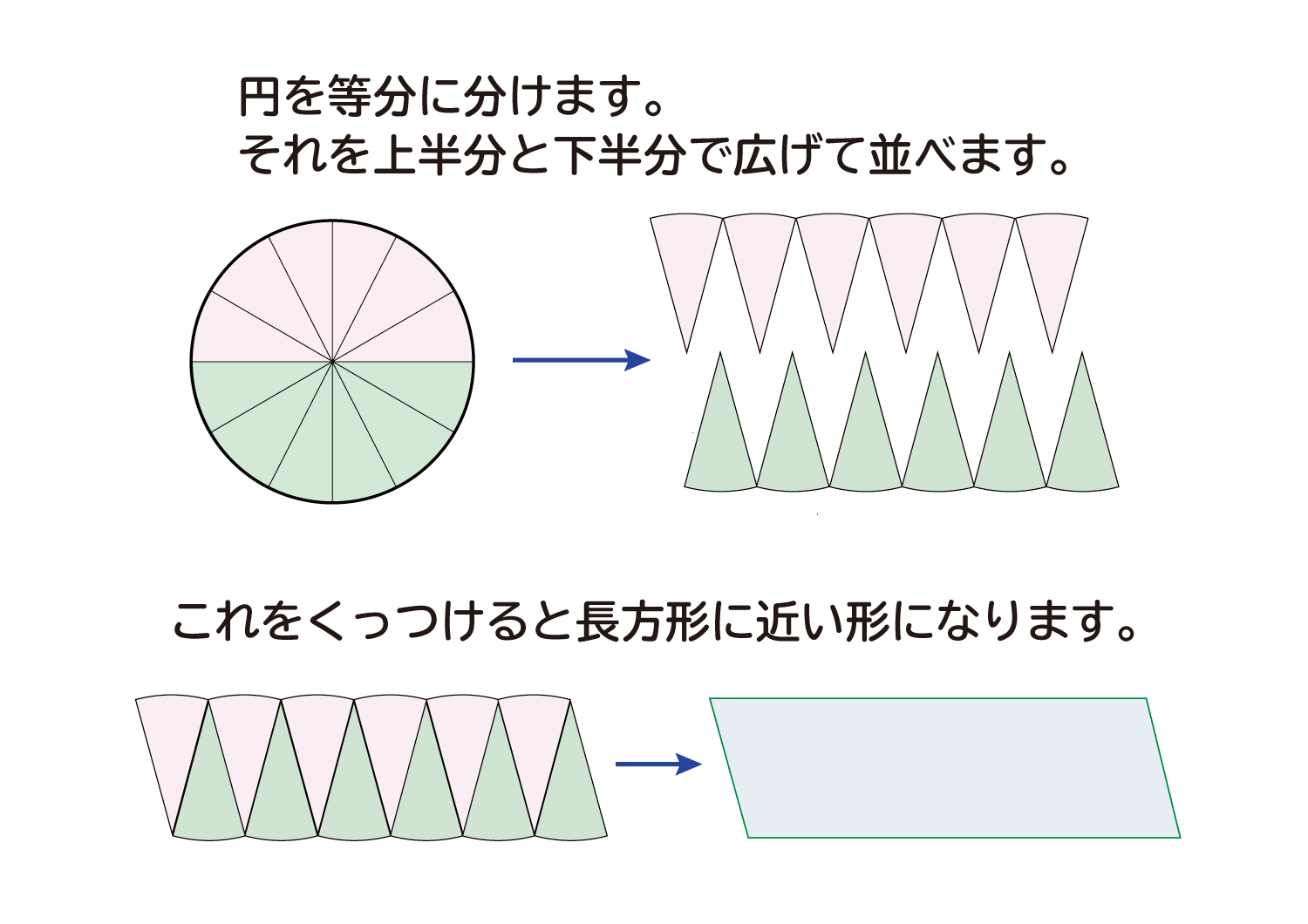
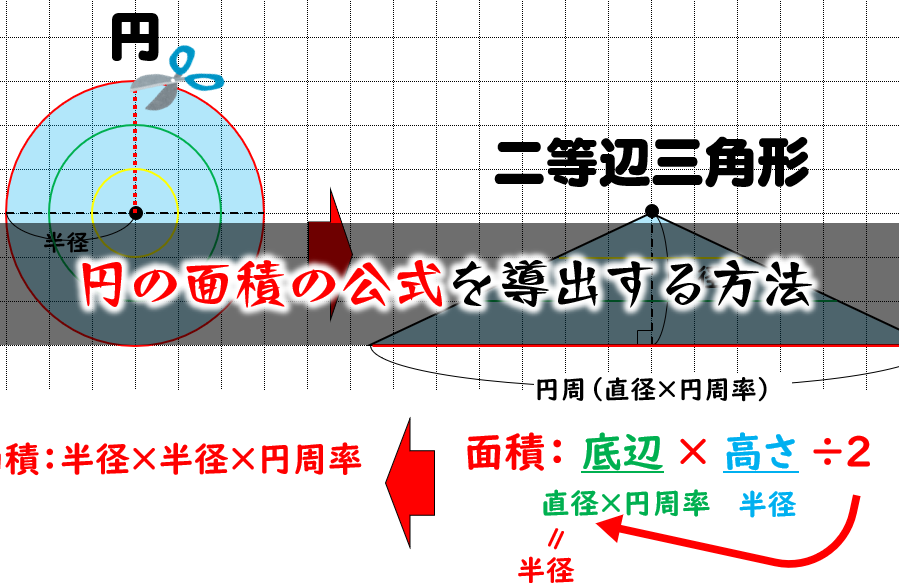
3 半径と円周率を利用し、円の面積を計算する 31 円の面積から、円の半径を計算する;ここで、S は円の面積、π は円周率、r は円の半径を表します。 このページの続きでは、この公式の導き方のイメージと、円の面積を求める計算問題の解き方を説明しています。 小学生向けに文字を使わない説明もしているので、ぜひご覧ください。 >次の数は円周の長さです。それぞれの円の半径と長さと面積を求めよ。 2512㎝ 半径をxcmと置いて、円周の長さに関する方程式を立ててみよう。 半径x2x円周率=円周の長さ ってね。半径がもとまったらあとは円の面積の公式で計算するだけ!
円 半径 求め方 座標のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 3 |  3 |  3 |
 3 |  3 | 3 |
 3 | 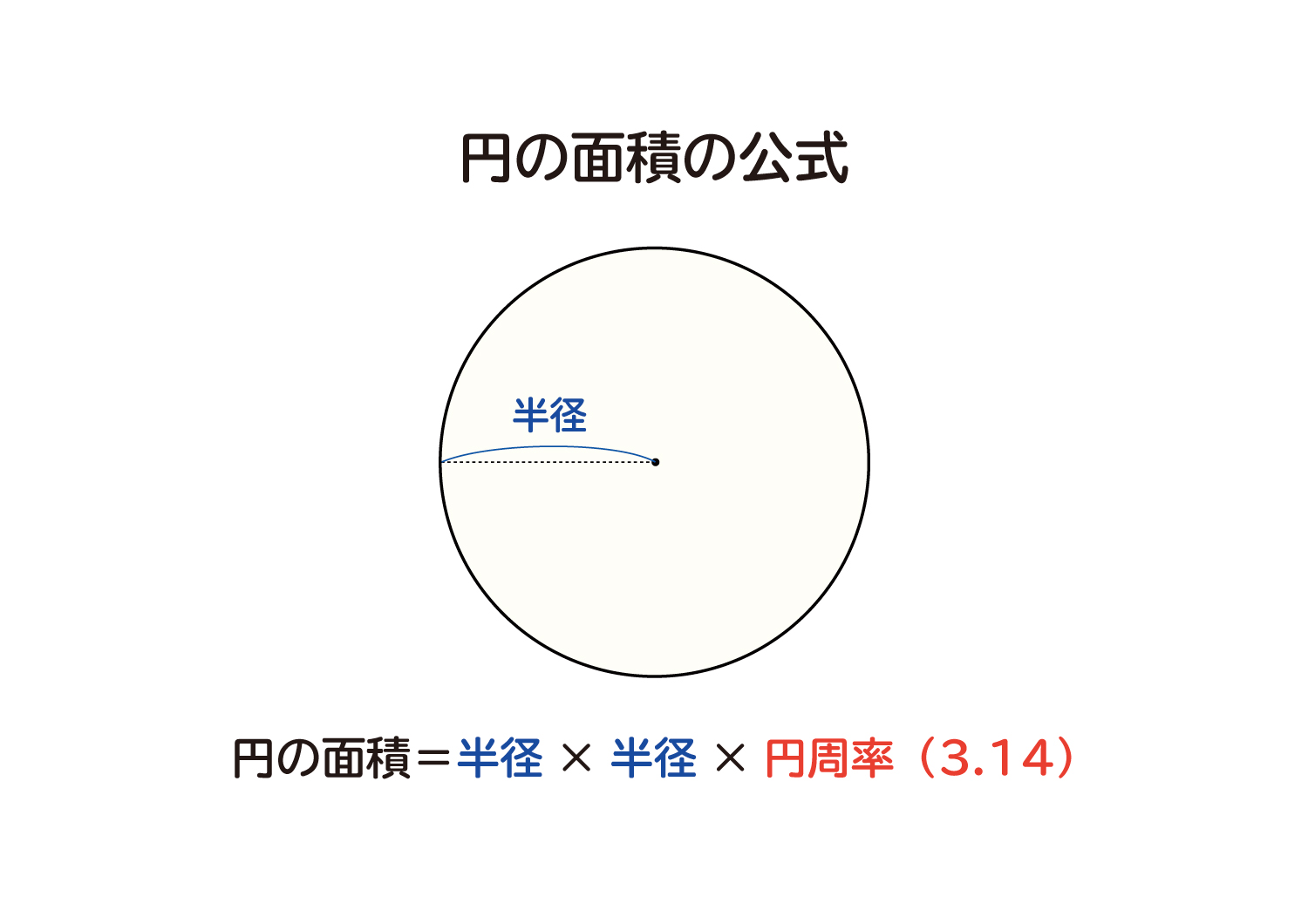 3 | 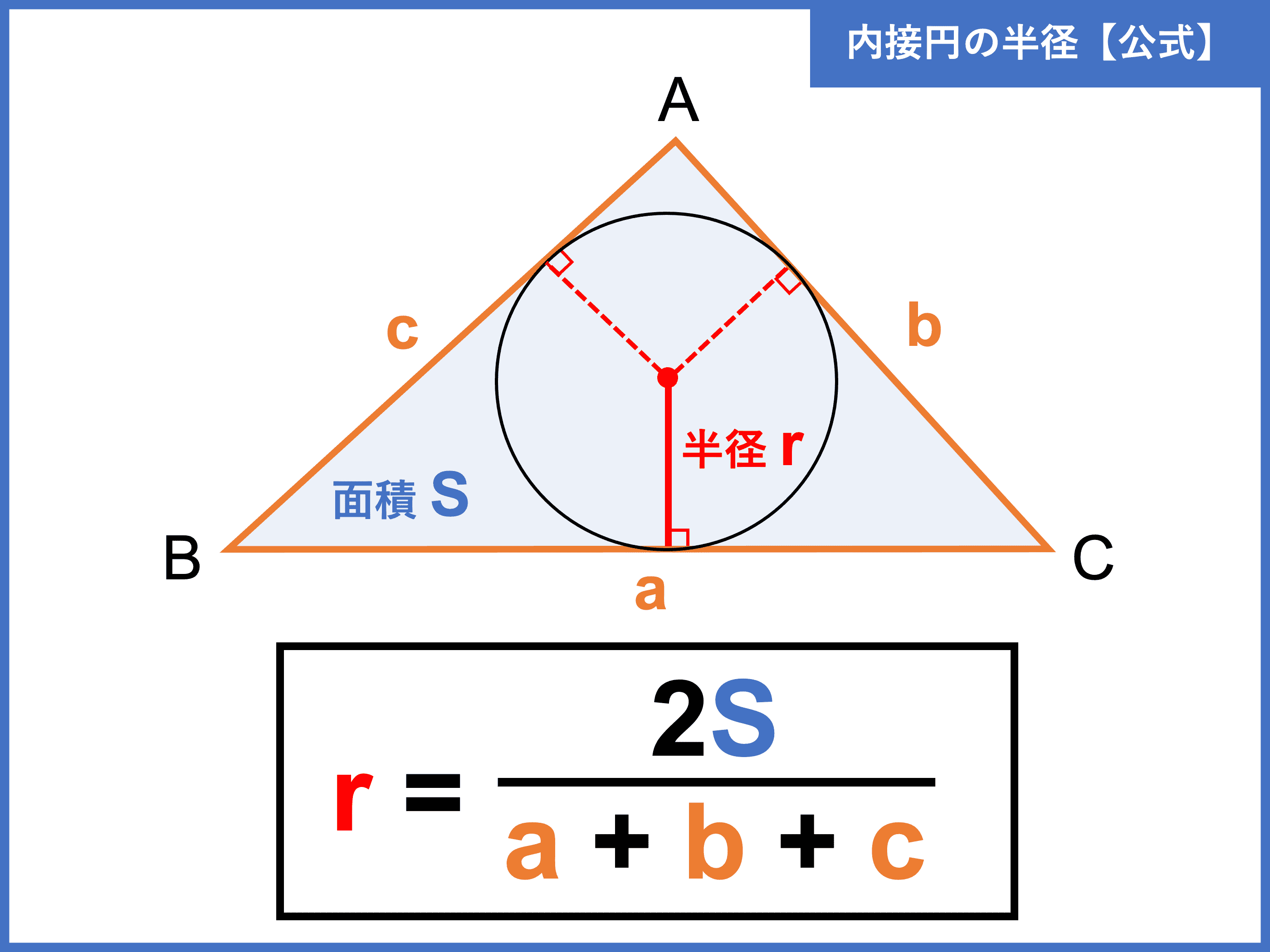 3 |
 3 |  3 | 3 |
3 |  3 |  3 |
 3 | 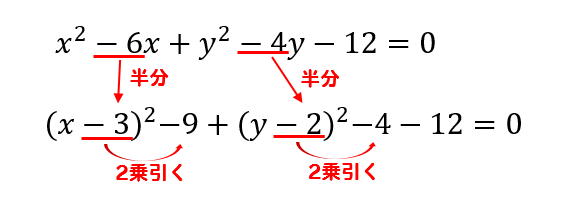 3 |  3 |
 3 | 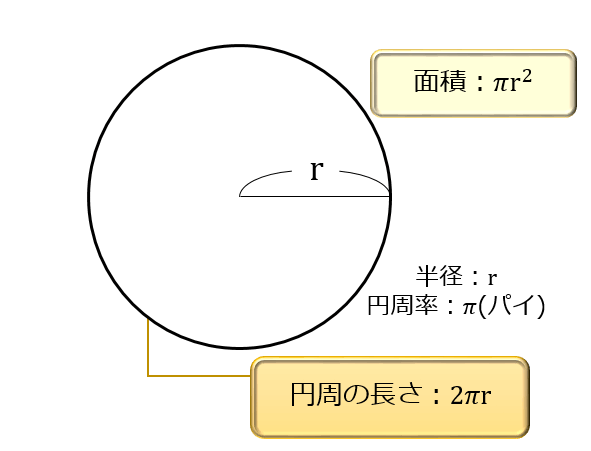 3 | 3 |
 3 |  3 | 3 |
 3 | 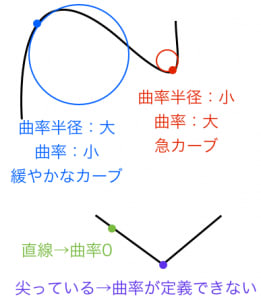 3 | 3 |
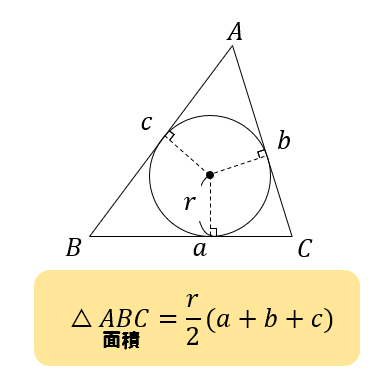 3 |  3 |  3 |
 3 | 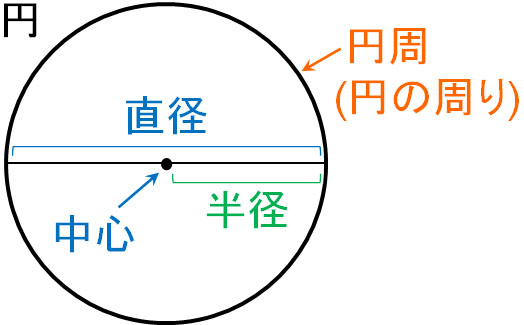 3 | 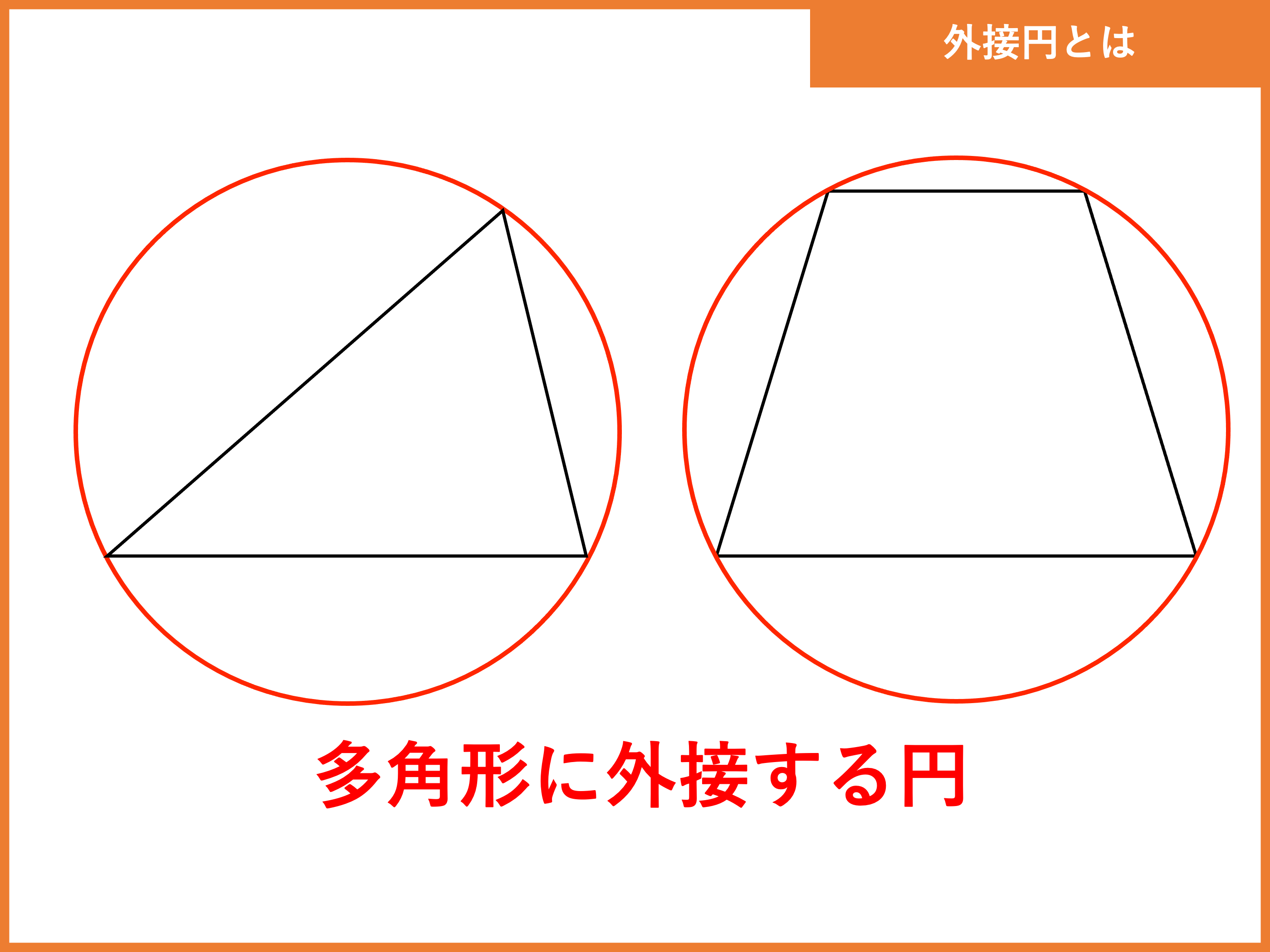 3 |
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 | 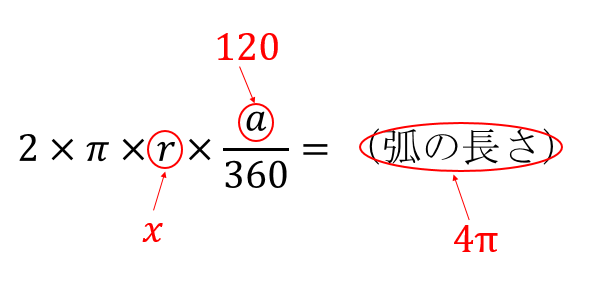 3 |  3 |
 3 |  3 | 3 |
3 |  3 |  3 |
 3 |  3 |  3 |
3 |  3 |  3 |
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 |  3 | 3 |
 3 | 3 |  3 |
3 | 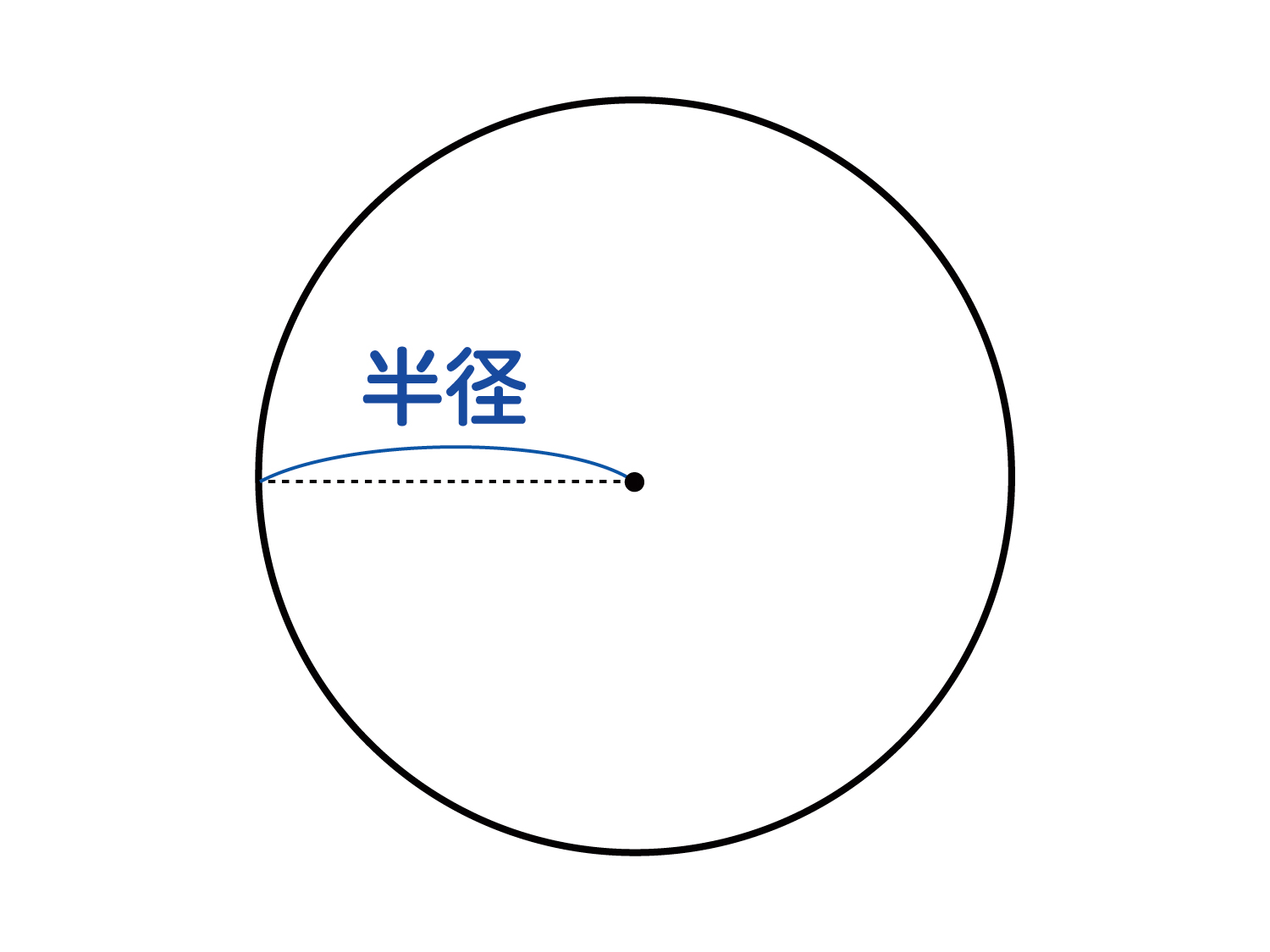 3 | 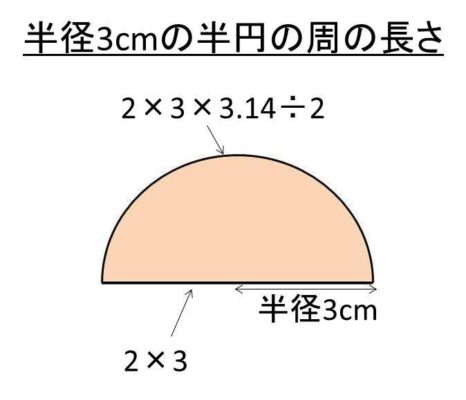 3 |
 3 | 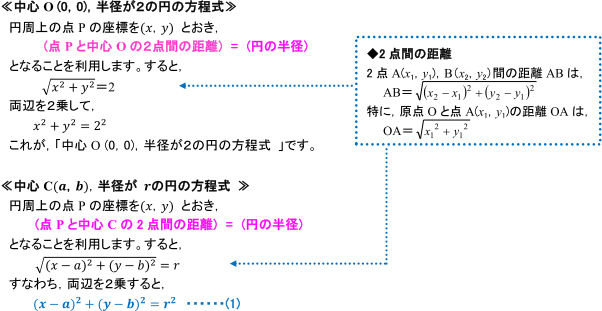 3 |  3 |
 3 | 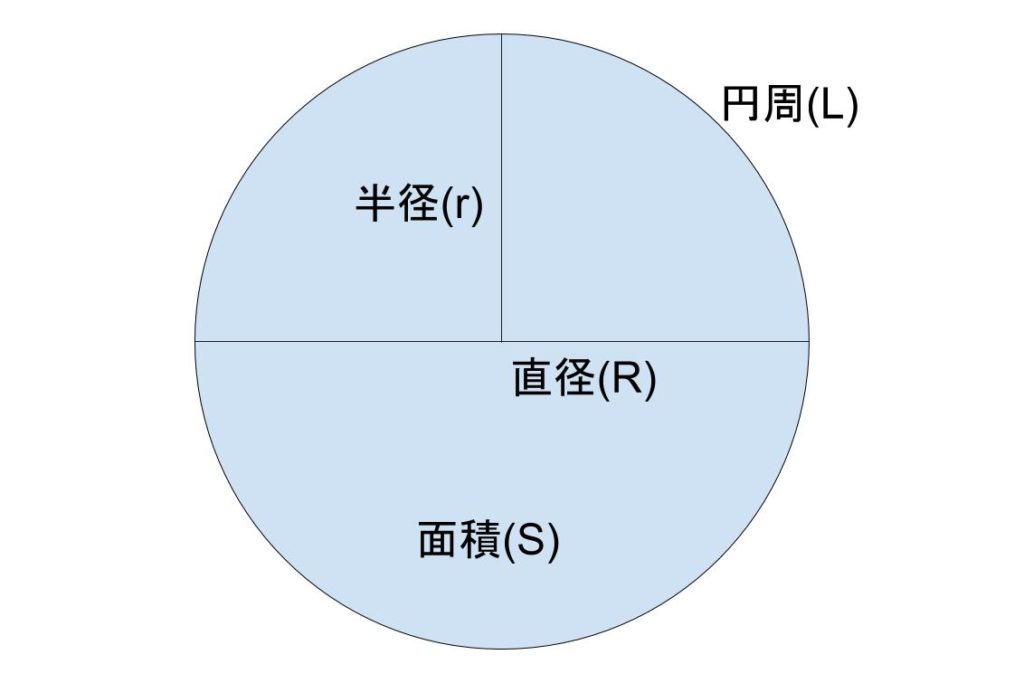 3 |  3 |
 3 | 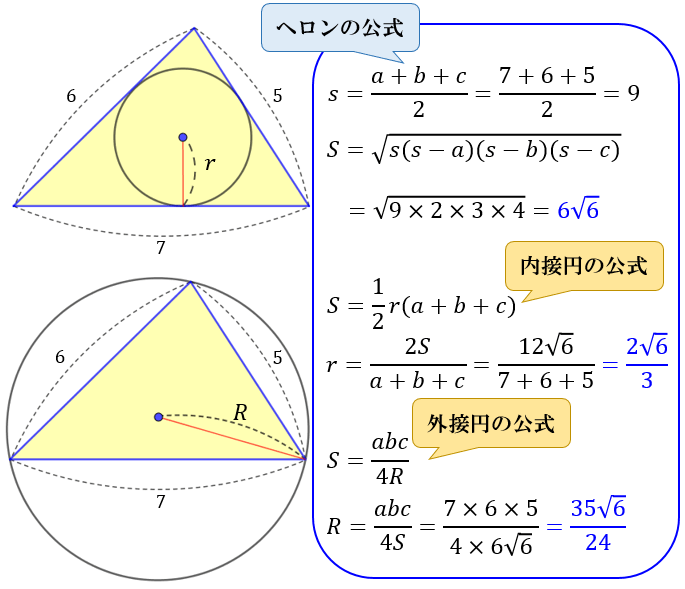 3 | 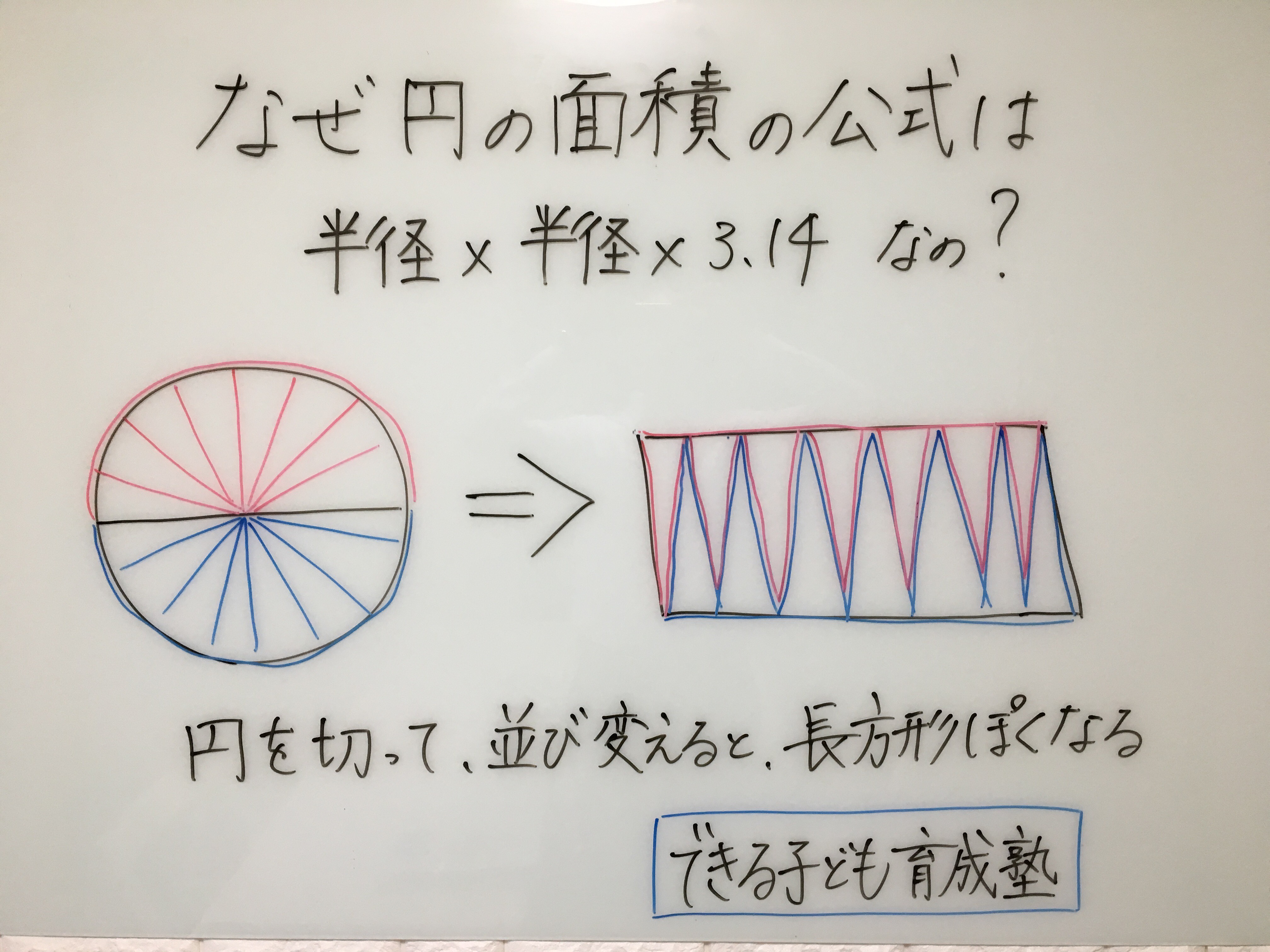 3 |
 3 |  3 | 3 |
 3 |  3 |  3 |
 3 |  3 | 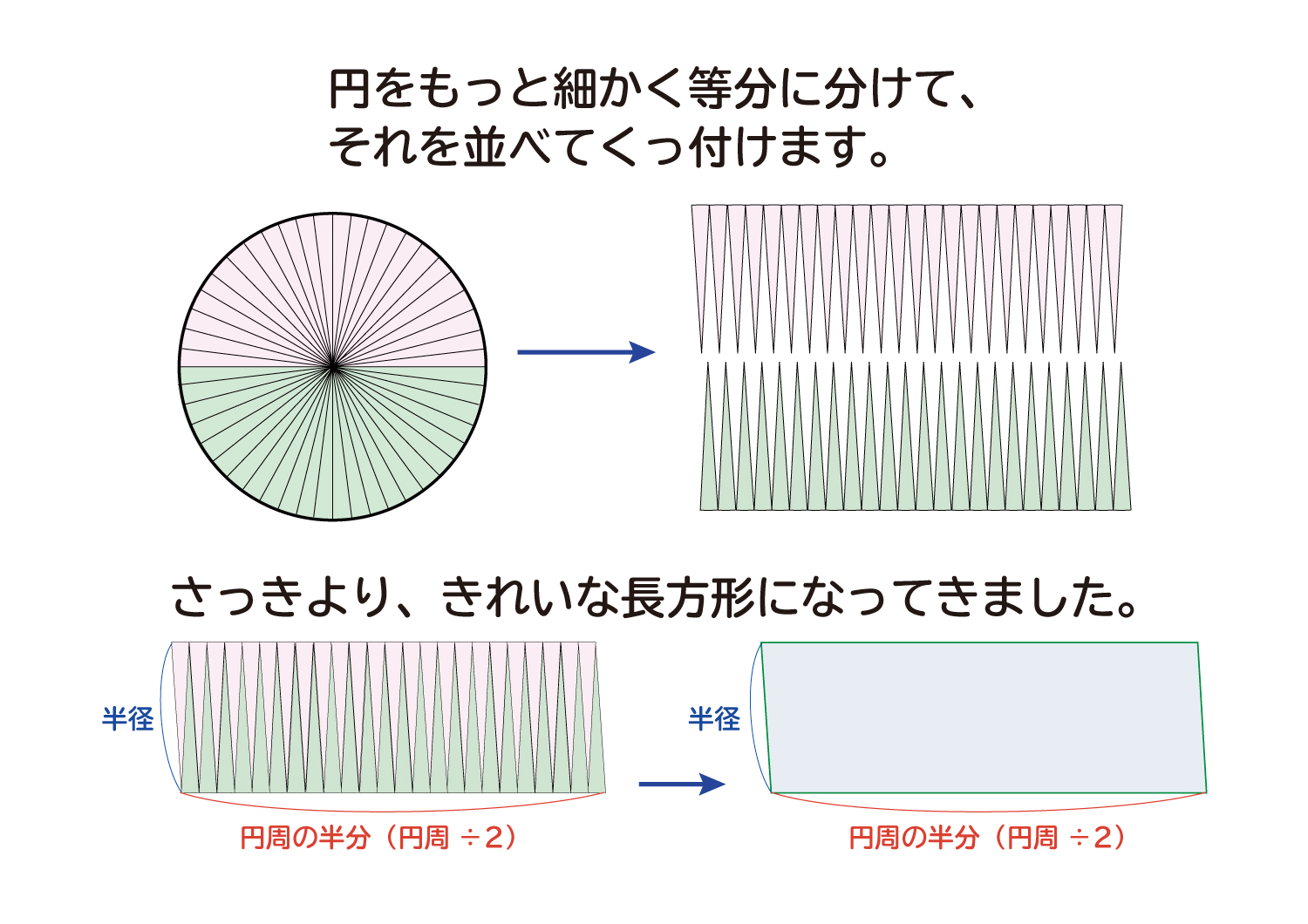 3 |
3 |  3 |  3 |
 3 |  3 |
について問題解説をしていくよ! 今回取り上げる問題はこちらだ! (1)中心が原点で、半径2の円 (2)中心 で、半径5の円 (3)中心 で、 軸に接する円 (4)中心 で、 軸に接する円 (5)中心 で、点 を通る円 (6)2点 、 を直径の両端とする円 (7 図の弧、弦の長さがわかっている状態で円の半径を求める式を探しているのですが なかなか見つける事ができません。 アプリで弧、弦で半径をもとめたいので公式? 求め方をご教示ください。 補足です。 実際に半径を求める式が知りたいです。 仮に
Incoming Term: 円 半径 求め方, 円 半径 求め方 座標,




0 件のコメント:
コメントを投稿